In this week’s issue and here online (see Fact), Richard Preston writes about how two mathematicians, Gregory and David Chudnovsky, came to the aid of the Metropolitan Museum for a project involving the legendary Unicorn tapestries. In this piece from 1992, Preston profiles the Chudnovskys, who were then engaged in an exploration of pi, one of the most mysterious numbers in mathematics.

Gregory Volfovich Chudnovsky recently built a supercomputer in his apartment from mail-order parts. Gregory Chudnovsky is a number theorist. His apartment is situated near the top floor of a run-down building on the West Side of Manhattan, in a neighborhood near Columbia University. Not long ago, a human corpse was found dumped at the end of the block. The world’s most powerful supercomputers include the Cray Y-MP C90, the Thinking Machines CM-5, the Hitachi S-820/80, the nCube, the Fujitsu parallel machine, the Kendall Square Research parallel machine, the nec SX-3, the Touchstone Delta, and Gregory Chudnovsky’s apartment. The apartment seems to be a kind of container for the supercomputer at least as much as it is a container for people.

Gregory Chudnovsky’s partner in the design and construction of the supercomputer was his older brother, David Volfovich Chudnovsky, who is also a mathematician, and who lives five blocks away from Gregory. The Chudnovsky brothers call their machine m zero. It occupies the former living room of Gregory’s apartment, and its tentacles reach into other rooms. The brothers claim that m zero is a “true, general-purpose supercomputer,” and that it is as fast and powerful as a somewhat older Cray Y-MP, but it is not as fast as the latest of the Y-MP machines, the C90, an advanced supercomputer made by Cray Research. A Cray Y-MP C90 costs more than thirty million dollars. It is a black monolith, seven feet tall and eight feet across, in the shape of a squat cylinder, and is cooled by liquid freon. So far, the brothers have spent around seventy thousand dollars on parts for their supercomputer, and much of the money has come out of their wives’ pockets.

Gregory Chudnovsky is thirty-nine years old, and he has a spare frame and a bony, handsome face. He has a long beard, streaked with gray, and dark, unruly hair, a wide forehead, and wide-spaced brown eyes. He walks in a slow, dragging shuffle, leaning on a bentwood cane, while his brother, David, typically holds him under one arm, to prevent him from toppling over. He has severe myasthenia gravis, an auto-immune disorder of the muscles. The symptoms, in his case, are muscular weakness and difficulty in breathing. “I have to lie in bed most of the time,” Gregory once told me. His condition doesn’t seem to be getting better, and doesn’t seem to be getting worse. He developed the disease when he was twelve years old, in the city of Kiev, Ukraine, where he and David grew up. He spends his days sitting or lying on a bed heaped with pillows, in a bedroom down the hall from the room that houses the supercomputer. Gregory’s bedroom is filled with paper; it contains at least a ton of paper. He calls the place his junk yard. The room faces east, and would be full of sunlight in the morning if he ever raised the shades, but he keeps them lowered, because light hurts his eyes.

You almost never meet one of the Chudnovsky brothers without the other. You often find the brothers conjoined, like Siamese twins, David holding Gregory by the arm or under the armpits. They complete each other’s sentences and interrupt each other, but they don’t look alike. While Gregory is thin and bearded, David has a stout body and a plump, clean-shaven face. He is in his early forties. Black-and-gray curly hair grows thickly on top of David’s head, and he has heavy-lidded deep-blue eyes. He always wears a starched white shirt and, usually, a gray silk necktie in a foulard print. His tie rests on a bulging stomach.

The Chudnovskian supercomputer, m zero, burns two thousand watts of power, and it runs day and night. The brothers don’t dare shut it down; if they did, it might die. At least twenty-five fans blow air through the machine to keep it cool; otherwise something might melt. Waste heat permeates Gregory’s apartment, and the room that contains m zero climbs to a hundred degrees Fahrenheit in summer. The brothers keep the apartment’s lights turned off as much as possible. If they switched on too many lights while m zero was running, they might blow the apartment’s wiring. Gregory can’t breathe city air without developing lung trouble, so he keeps the apartment’s windows closed all the time, with air-conditioners running in them during the summer, but that doesn’t seem to reduce the heat, and as the temperature rises inside the apartment the place can smell of cooking circuit boards, a sign that m zero is not well. A steady stream of boxes arrives by Federal Express, and an opposing stream of boxes flows back to mail-order houses, containing parts that have bombed, along with letters from the brothers demanding an exchange or their money back. The building superintendent doesn’t know that the Chudnovsky brothers have been using a supercomputer in Gregory’s apartment, and the brothers haven’t expressed an eagerness to tell him.

The Chudnovskys, between them, have published a hundred and fifty-four papers and twelve books, mostly in collaboration with each other, and mostly on the subject of number theory or mathematical physics. They work together so closely that it is possible to argue that they are a single mathematician—anyway, it’s what they claim. The brothers lived in Kiev until 1977, when they left the Soviet Union and, accompanied by their parents, went to France. The family lived there for six months, then emigrated to the United States and settled in New York; they have become American citizens.

The brothers enjoy an official relationship with Columbia University: Columbia calls them senior research scientists in the Department of Mathematics, but they don’t have tenure and they don’t teach students. They are really lone inventors, operating out of Gregory’s apartment in what you might call the old-fashioned Russo-Yankee style. Their wives are doing well. Gregory’s wife, Christine Pardo Chudnovsky, is an attorney with a midtown law firm. David’s wife, Nicole Lannegrace, is a political-affairs officer at the United Nations. It is their salaries that help cover the funding needs of the brothers’ supercomputing complex in Gregory and Christine’s apartment. Malka Benjaminovna Chudnovsky, a retired engineer, who is Gregory and David’s mother, lives in Gregory’s apartment. David spends his days in Gregory’s apartment, taking care of his brother, their mother, and m zero.

When the Chudnovskys applied to leave the Soviet Union, the fact that they are Jewish and mathematical attracted at least a dozen K.G.B. agents to their case. The brothers’ father, Volf Grigorevich Chudnovsky, who was severely beaten by the K.G.B. in 1977, died of heart failure in 1985. Volf Chudnovsky was a professor of civil engineering at the Kiev Architectural Institute, and he specialized in the structural stability of buildings, towers, and bridges. He died in America, and not long before he died he constructed in Gregory’s apartment a maze of bookshelves, his last work of civil engineering. The bookshelves extend into every corner of the apartment, and today they are packed with literature and computer books and books and papers on the subject of numbers. Since almost all numbers run to infinity (in digits) and are totally unexplored, an apartmentful of thoughts about numbers holds hardly any thoughts at all, even with a supercomputer on the premises to advance the work.

The brothers say that the “m” in “m zero” stands for “machine,” and that they use a small letter to imply that the machine is a work in progress. They represent the name typographically as “m0.” The “zero” stands for success. It implies a dark history of failure—three duds (in Gregory’s apartment) that the brothers now refer to as negative three, negative two, and negative one. The brothers broke up the negative machines for scrap, got on the telephone, and waited for Federal Express to bring more parts.

M zero is a parallel supercomputer, a type of machine that has lately come to dominate the avant-garde in supercomputer architecture, because the design offers succulent possibilities for speed in solving problems. In a parallel machine, anywhere from half a dozen to thousands of processors work simultaneously on a problem, whereas in a so-called serial machine—a normal computer—the problem is solved one step at a time. “A serial machine is bound to be very slow, because the speed of the machine will be limited by the slowest part of it,” Gregory said. “In a parallel machine, many circuits take on many parts of the problem at the same time.” As of last week, m zero contained sixteen parallel processors, which ruminate around the clock on the Chudnovskys’ problems.

The brothers’ mail-order supercomputer makes their lives more convenient: m zero performs inhumanly difficult algebra, finding roots of gigantic systems of equations, and it has constructed colored images of the interior of Gregory Chudnovsky’s body. According to the Chudnovskys, it could model the weather or make pictures of air flowing over a wing, if the brothers cared about weather or wings. What they care about is numbers. To them, numbers are more beautiful, more nearly perfect, possibly more complicated, and arguably more real than anything in the world of physical matter.

The brothers have lately been using m zero to explore the number pi. Pi, which is denoted by the Greek letter ?, is the most famous ratio in mathematics, and is one of the most ancient numbers known to humanity. Pi is approximately 3.14—the number of times that a circle’s diameter will fit around the circle. Here is a circle, with its diameter:

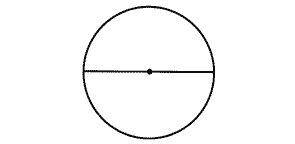
Pi goes on forever, and can’t be calculated to perfect precision: 3.14159265358979323846264338 32795028841971693993751 . . . . This is known as the decimal expansion of pi. It is a bloody mess. No apparent pattern emerges in the succession of digits. The digits of pi march to infinity in a predestined yet unfathomable code: they do not repeat periodically, seeming to pop up by blind chance, lacking any perceivable order, rule, reason, or design—“random” integers, ad infinitum. If a deep and beautiful design hides in the digits of pi, no one knows what it is, and no one has ever been able to see it by staring at the digits. Among mathematicians, there is a nearly universal feeling that it will never be possible, in principle, for an inhabitant of our finite universe to discover the system in the digits of pi. But for the present, if you want to attempt it, you need a supercomputer to probe the endless scrap of leftover pi.

Before the Chudnovsky brothers built m zero, Gregory had to derive pi over the telephone network while lying in bed. It was inconvenient. Tapping at a small keyboard, which he sets on the blankets of his bed, he stares at a computer display screen on one of the bookshelves beside his bed. The keyboard and the screen are connected to Internet, a network that leads Gregory through cyberspace into the heart of a Cray somewhere else in the United States. He calls up a Cray through Internet and programs the machine to make an approximation of pi. The job begins to run, the Cray trying to estimate the number of times that the diameter of a circle goes around the periphery, and Gregory sits back on his pillows and waits, watching messages from the Cray flow across his display screen. He eats dinner with his wife and his mother and then, back in bed, he takes up a legal pad and a red felt-tip pen and plays with number theory, trying to discover hidden properties of numbers. Meanwhile, the Cray is reaching toward pi at a rate of a hundred million operations per second. Gregory dozes beside his computer screen. Once in a while, he asks the Cray how things are going, and the Cray replies that the job is still active. Night passes, the Cray running deep toward pi. Unfortunately, since the exact ratio of the circle’s circumference to its diameter dwells at infinity, the Cray has not even begun to pinpoint pi. Abruptly, a message appears on Gregory’s screen:

LINE IS DISCONNECTED.

“What the hell is going on?” Gregory exclaims. It seems that the Cray has hung up the phone, and may have crashed. Once again, pi has demonstrated its ability to give a supercomputer a heart attack.

"Myasthenia gravis is a funny thing,” Gregory Chudnoysky said one day from his bed in the junk yard. “In a sense, I’m very lucky, because I’m alive, and I’m alive after so many years.” He has a resonant voice and a Russian accent. “There is no standard prognosis. It sometimes strikes young women and older women. I wonder if it is some kind of sluggish virus.”

It was a cold afternoon, and rain pelted the windows; the shades were drawn, as always. He lay against a heap of pillows, with his legs folded under him. He wore a tattered gray lamb’s-wool sweater that had multiple patches on the elbows, and a starched white shirt, and baggy blue sweatpants, and a pair of handmade socks. I had never seen socks like Gregory’s. They were two-tone socks, wrinkled and floppy, hand-sewn from pieces of dark-blue and pale-blue cloth, and they looked comfortable. They were the work of Malka Benjaminovna, his mother. Lines of computer code flickered on the screen beside his bed.

This was an apartment built for long voyages. The paper in the room was jammed into the bookshelves, from floor to ceiling. The brothers had wedged the paper, sheet by sheet, into manila folders, until the folders had grown as fat as melons. The paper also flooded two freestanding bookshelves (placed strategically around Gregory’s bed), five chairs (three of them in a row beside his bed), two steamer trunks, and a folding cocktail table. I moved carefully around the room, fearful of triggering a paperslide, and sat on the room’s one empty chair, facing the foot of Gregory’s bed, my knees touching the blanket. The paper was piled in three-foot stacks on the chairs. It guarded his bed like the flanking towers of a fortress, and his bed sat at the center of the keep. I sensed a profound happiness in Gregory Chudnovsky’s bedroom. His happiness, it occurred to me later, sprang from the delicious melancholy of a life chained to a bed in a disordered world that breaks open through the portals of mathematics into vistas beyond time or decay.

“The system of this paper is archeological,” he said. “By looking at a slice, I know the year. This slice is 1986. Over here is some 1985. What you see in this room is our working papers, as well as the papers we used as references for them. Some of the references we pull out once in a while to look at, and then we leave them somewhere else, in another pile. Once, we had to make a Xerox copy of a book three times, and we put it in three different places in the piles, so we would be sure to find it when we needed it. Unfortunately, once we put a book into one of these piles we almost never go back to look for it. There are books in there by Kipling and Macaulay. Actually, when we want to find a book it’s easier to go back to the library. Eh, this place is a mess. Eventually, these papers or my wife will turn me out of the house.”

Much of the paper consists of legal pads covered with Gregory’s handwriting. His holograph is dense and careful, a flawless minuscule written with a red felt-tip pen—a mixture of theorems, calculations, proofs, and conjectures concerning numbers. He uses a felt-tip pen because he doesn’t have enough strength in his hand to press a pencil on paper. Mathematicians who have visited Gregory Chudnovsky’s bedroom have come away dizzy, wondering what secrets the scriptorium may hold. Some say he has published most of his work, while others wonder if his bedroom holds unpublished discoveries. He cautiously refers to his steamer trunks as valises. They are filled to the lids with compressed paper. When Gregory and David used to fly to Europe to speak at conferences, they took both “valises” with them, in case they needed to refer to a theorem, and the baggage particularly annoyed the Belgians. “The Belgians were always fining us for being overweight,” Gregory said.

Pi is by no means the only unexplored number in the Chudnovskys’ inventory, but it is one that interests them very much. They wonder whether the digits contain a hidden rule, an as yet unseen architecture, close to the mind of God. A subtle and fantastic order may appear in the digits of pi way out there somewhere; no one knows. No one has ever proved, for example, that pi does not turn into nothing but nines and zeros, spattered to infinity in some peculiar arrangement. If we were to explore the digits of pi far enough, they might resolve into a breathtaking numerical pattern, as knotty as “The Book of Kells,” and it might mean something. It might be a small but interesting message from God, hidden in the crypt of the circle, awaiting notice by a mathematician. On the other hand, the digits of pi may ramble forever in a hideous cacophony, which is a kind of absolute perfection to a mathematician like Gregory Chudnovsky. Pi looks “monstrous” to him. “We know absolutely nothing about pi,” he declared from his bed. “What the hell does it mean? The definition of pi is really very simple—it’s just the ratio of the circumference to the diameter—but the complexity of the sequence it spits out in digits is really unbelievable. We have a sequence of digits that looks like gibberish.”

“Maybe in the eyes of God pi looks perfect,” David said, standing in a corner of the room, his head and shoulders visible above towers of paper.

Pi, or ?, has had various names through the ages, and all of them are either words or abstract symbols, since pi is a number that can’t be shown completely and exactly in any finite form of representation. Pi is a transcendental number. A transcendental number is a number that exists but can’t be expressed in any finite series of either arithmetical or algebraic operations. For example, if you try to express pi as the solution to an equation you will find that the equation goes on forever. Expressed in digits, pi extends into the distance as far as the eye can see, and the digits never repeat periodically, as do the digits of a rational number. Pi slips away from all rational methods used to locate it. Pi is a transcendental number because it transcends the power of algebra to display it in its totality. Ferdinand Lindemann, a German mathematician, proved the transcendence of pi in 1882; he proved, in effect, that pi can’t be written on a piece of paper, not even on a piece of paper as big as the universe. In a manner of speaking, pi is indescribable and can’t be found.

Pi possibly first entered human consciousness in Egypt. The earliest known reference to pi occurs in a Middle Kingdom papyrus scroll, written around 1650 B.C. by a scribe named Ahmes. Showing a restrained appreciation for his own work that is not uncommon in a mathematician, Ahmes began his scroll with the words “The Entrance Into the Knowledge of All Existing Things.” He remarked in passing that he composed the scroll “in likeness to writings made of old,” and then he led his readers through various mathematical problems and their solutions, along several feet of papyrus, and toward the end of the scroll he found the area of a circle, using a rough sort of pi.

Around 200 B.C., Archimedes of Syracuse found that pi is somewhere between 3 10/71, and 3 1/7—that’s about 3.14. (The Greeks didn’t use decimals.) Archimedes had no special term for pi, calling it “the perimeter to the diameter.” By in effect approximating pi to two places after the decimal point, Archimedes narrowed the known value of pi to one part in a hundred. There knowledge of pi bogged down until the seventeenth century, when new formulas for approximating pi were discovered. Pi then came to be called the Ludolphian number, after Ludolph van Ceulen, a German mathematician who approximated it to thirty-five decimal places, or one part in a hundred million billion billion billion—a calculation that took Ludolph most of his life to accomplish, and gave him such satisfaction that he had the digits engraved on his tombstone, at the Ladies’ Church in Leiden, in the Netherlands. Ludolph and his tombstone were later moved to Peter’s Church in Leiden, to be installed in a special graveyard for professors, and from there the stone vanished, possibly to be turned into a sidewalk slab. Somewhere in Leiden, people may be walking over Ludolph’s digits. The Germans still call pi the Ludolphian number. In the eighteenth century, Leonhard Euler, mathematician to Catherine the Great, called it p or c. The first person to use the Greek letter ? for the number was William Jones, an English mathematician, who coined it in 1706 for his book “A New Introduction to the Mathematics.” Euler read the book and switched to using the symbol ?, and the number has remained ? ever since. Jones probably meant ? to stand for the English word “periphery.”

Physicists have noted the ubiquity of pi in nature. Pi is obvious in the disks of the moon and the sun. The double helix of DNA revolves around pi. Pi hides in the rainbow, and sits in the pupil of the eye, and when a raindrop falls into water pi emerges in the spreading rings. Pi can be found in waves and ripples and spectra of all kinds, and therefore pi occurs in colors and music. Pi has lately turned up in superstrings, the hypothetical loops of energy vibrating inside subatomic particles. Pi occurs naturally in tables of death, in what is known as a Gaussian distribution of deaths in a population; that is, when a person dies, the event “feels” the Ludolphian number.

It is one of the great mysteries why nature seems to know mathematics. No one can suggest why this necessarily has to be so. Eugene Wigner, the physicist, once said, “The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.” We may not understand pi or deserve it, but nature at least seems to be aware of it, as Captain O. C. Fox learned while he was recovering in a hospital from a wound sustained in the American Civil War. Having nothing better to do with his time than lie in bed and derive pi, Captain Fox spent a few weeks tossing pieces of fine steel wire onto a wooden board ruled with parallel lines. The wires fell randomly across the lines in such a way that pi emerged in the statistics. After throwing his wires eleven hundred times, Captain Fox was able to derive pi to two places after the decimal point, to 3.14. If he had had a thousand years to recover from his wound, he might have derived pi to perhaps another decimal place. To go deeper into pi, you need a powerful machine.

The race toward pi happens in cyberspace, inside supercomputers. In 1949, George Reitwiesner, at the Ballistic Research Laboratory, in Maryland, derived pi to two thousand and thirty-seven decimal places with the eniac, the first general-purpose electronic digital computer. Working at the same laboratory, John von Neumann (one of the inventors of the eniac) searched those digits for signs of order, but found nothing he could put his finger on. A decade later, Daniel Shanks and John W. Wrench, Jr., approximated pi to a hundred thousand decimal places with an I.B.M. 7090 mainframe computer, and saw nothing. The race continued desultorily, through hundreds of thousands of digits, until 1981, when Yasumasa Kanada, the head of a team of computer scientists at Tokyo University, used a nec supercomputer, a Japanese machine, to compute two million digits of pi. People were astonished that anyone would bother to do it, but that was only the beginning of the affair. In 1984, Kanada and his team got sixteen million digits of pi, noticing nothing remarkable. A year later, William Gosper, a mathematician and distinguished hacker employed at Symbolics, Inc., in Sunnyvale, California, computed pi to seventeen and a half million decimal places with a Symbolics workstation, beating Kanada’s team by a million digits. Gosper saw nothing of interest.

The next year, David H. Bailey, at the National Aeronautics and Space Administration, used a Cray 2 supercomputer and a formula discovered by two brothers, Jonathan and Peter Borwein, to scoop twenty-nine million digits of pi. Bailey found nothing unusual. A year after that, in 1987, Yasumasa Kanada and his team got a hundred and thirty-four million digits of pi, using a nec SX-2 supercomputer. They saw nothing of interest. In 1988, Kanada kept going, past two hundred million digits, and saw further amounts of nothing. Then, in the spring of 1989, the Chudnovsky brothers (who had not previously been known to have any interest in calculating pi) suddenly announced that they had obtained four hundred and eighty million digits of pi—a world record—using supercomputers at two sites in the United States, and had seen nothing. Kanada and his team were a little surprised to learn of unknown competition operating in American cyberspace, and they got on a Hitachi supercomputer and ripped through five hundred and thirty-six million digits, beating the Chudnovksys, setting a new world record, and seeing nothing. The brothers kept calculating and soon cracked a billion digits, but Kanada’s restless boys and their Hitachi then nosed into a little more than a billion digits. The Chudnovskys pressed onward, too, and by the fall of 1989 they had squeaked past Kanada again, having computed pi to one billion one hundred and thirty million one hundred and sixty thousand six hundred and sixty-four decimal places, without finding anything special. It was another world record. At that point, the brothers gave up, out of boredom.

If a billion decimals of pi were printed in ordinary type, they would stretch from New York City to the middle of Kansas. This notion raises the question: What is the point of computing pi from New York to Kansas? The question has indeed been asked among mathematicians, since an expansion of pi to only forty-seven decimal places would be sufficiently precise to inscribe a circle around the visible universe that doesn’t deviate from perfect circularity by more than the distance across a single proton. A billion decimals of pi go so far beyond that kind of precision, into such a lunacy of exactitude, that physicists will never need to use the quantity in any experiment—at least, not for any physics we know of today—and the thought of a billion decimals of pi oppresses even some mathematicians, who declare the Chudnovskys’ effort trivial. I once asked Gregory if a certain impression I had of mathematicians was true, that they spent immoderate amounts of time declaring each other’s work trivial. “It is true,” he admitted. “There is actually a reason for this. Because once you know the solution to a problem it usually is trivial.”

Gregory did the calculation from his bed in New York, working through cyberspace on a Cray 2 at the Minnesota Supercomputer Center, in Minneapolis, and on an I.B.M. 3090-VF supercomputer at the I.B.M. Thomas J. Watson Research Center, in Yorktown Heights, New York. The calculation triggered some dramatic crashes, and took half a year, because the brothers could get time on the supercomputers only in bits and pieces, usually during holidays and in the dead of night. It was also quite expensive—the use of the Cray cost them seven hundred and fifty dollars an hour, and the money came from the National Science Foundation. By the time of this agony, the brothers had concluded that it would be cheaper and more convenient to build a supercomputer in Gregory’s apartment. Then they could crash their own machine all they wanted, while they opened doors in the house of numbers. The brothers planned to compute two billion digits of pi on their new machine to try to double their old world record. They thought it would be a good way to test their supercomputer: a maiden voyage into pi would put a terrible strain on their machine, might blow it up. Presuming that their machine wouldn’t overheat or strangle on digits, they planned to search the huge resulting string of pi for signs of hidden order. If what the Chudnovsky brothers have seen in the Ludolphian number is a message from God, the brothers aren’t sure what God is trying to say.

On a cold winter day, when the Chudnovskys were about to begin their two-billion-digit expedition into pi, I rang the bell of Gregory Chudnovsky’s apartment, and David answered the door. He pulled the door open a few inches, and then it stopped, jammed against an empty cardboard box and a wad of hanging coats. He nudged the box out of the way with his foot. “Look, don’t worry,” he said. “Nothing unpleasant will happen to you. We will not turn you into digits.” A Mini Mag-Lite flashlight protruded from his shirt pocket.

We were standing in a long, dark hallway. The lights were off, and it was hard to see anything. To try to find something in Gregory’s apartment is like spelunking; that was the reason for David’s flashlight. The hall is lined on both sides with bookshelves, and they hold a mixture of paper and books. The shelves leave a passage about two feet wide down the length of the hallway. At the end of the hallway is a French door, its mullioned glass covered with translucent paper, and it glowed.

The apartment’s rooms are strung out along the hallway. We passed a bathroom and a bedroom. The bedroom belonged to Malka Benjaminovna Chudnovsky. We passed a cave of paper, Gregory’s junk yard. We passed a small kitchen, our feet rolling on computer cables. David opened the French door, and we entered the room of the supercomputer. A bare light bulb burned in a ceiling fixture. The room contained seven display screens: two of them were filled with numbers; the others were turned off. The windows were closed and the shades were drawn. Gregory Chudnovsky sat on a chair facing the screens. He wore the usual outfit—a tattered and patched lamb’s-wool sweater, a starched white shirt, blue sweatpants, and the hand-stitched two-tone socks. From his toes trailed a pair of heelless leather slippers. His cane was hooked over his shoulder, hung there for convenience. I shook his hand. “Our first goal is to compute pi,” he said. “For that we have to build our own computer.”

“We are a full-service company,” David said. “Of course, you know what ‘full-service’ means in New York. It means ‘You want it? You do it yourself.’ ”

A steel frame stood in the center of the room, screwed together with bolts. It held split shells of mail-order personal computers—cheap P.C. clones, knocked wide open, like cracked walnuts, their meat spilling all over the place. The brothers had crammed special logic boards inside the personal computers. Red lights on the boards blinked. The floor was a quagmire of cables.

The brothers had also managed to fit into the room masses of empty cardboard boxes, and lots of books (Russian classics, with Cyrillic lettering on their spines), and screwdrivers, and data-storage tapes, and software manuals by the cubic yard, and stalagmites of obscure trade magazines, and a twenty-thousand-dollar computer workstation that the brothers no longer used. (“We use it as a place to stack paper,” Gregory said.) From an oval photograph on the wall, the face of their late father—a robust man, squinting thoughtfully—looked down on the scene. The walls andthe French door were covered with sheets of drafting paper showing circuit diagrams. They resembled cities seen from the air: the brothers had big plans for m zero. Computer disk drives stood around the room. The drives hummed, and there was a continuous whirr of fans, and a strong warmth emanated from the equipment, as if a steam radiator were going in the room. The brothers heat their apartment largely with chips.

Gregory said, “Our knowledge of pi was barely in the millions of digits—”

“We need many billions of digits,” David said. “Even a billion digits is a drop in the bucket. Would you like a Coca-Cola?” He went into the kitchen and there was a horrible crash. “Never mind, I broke a glass,” he called. “Look, it’s not a problem.” He came out of the kitchen carrying a glass of Coca-Cola on a tray, with a paper napkin under the glass, and as he handed it to me he urged me to hold it tightly, because a Coca-Cola spilled into— He didn’t want to think about it; it would set back the project by months. He said, “Galileo had to build his telescope—”

“Because he couldn’t afford the Dutch model,” Gregory said.

“And we have to build our machine because we have—”

“No money,” Gregory said. “When people let us use their computer, it’s always done as a kindness.” He grinned and pinched his finger and thumb together. “They say, ‘You can use it as long a nobody complains.’ ”

I asked the brothers when they planned to build their supercomputer.

They burst out laughing. “You are sitting inside it!” David roared.

“Tell us how a supercomputer should look,” Gregory said.

I started to describe a Cray to the brothers.

David turned to his brother an said, “The interviewer answers our questions. It’s Pirandello! The interviewer becomes a person in the story.” David turned to me and said, “The problem is, you should change you thinking. If I were to put inside this Cray a chopped-meat machine, you wouldn’t know it was a meat chopper.”

“Unless you saw chopped meat coming out of it. Then you’d suspect it wasn’t a Cray,” Gregory said, and the brothers cackled.

“In ten years, a Cray will fit in your pocket,” David said.

Supercomputers are evolving incredibly fast. The notion of what a supercomputer is and what it can do changes from year to year, if not from month to month, as new machines arise. The definition of a supercomputer is simply this: one of the fastest and most powerful scientific computers in the world for its time. The power of a supercomputer is revealed, generally speaking, in its ability to solve tough problems. A Cray Y-MP8, running at peak working speed, can perform more than two billion floating-point operations per second. Floating-point operations—or flops, as they are called—are a standard measure of speed. Since Cray Y-MP8 can hit two and a half billion flops, it is considered to be gigaflop supercomputer. Giga (from the Greek for “giant”) means a billion. Like all supercomputers, a Cray often cruises along significantly below its peak working speed. (There is a heated controversy in the supercomputer industry over how to measure the typical working performance of any given supercomputer, and there are many claims and counterclaims.) A Cray is a so-called vector-processing machine, but that design is going out of fashion. Cray Research has announced that next year it will begin selling an even more powerful parallel machine.

“Our machine is a gigaflop supercomputer,” David Chudnovsky told me. “The working speed of our machine is from two hundred million flops to two gigaflops—roughly in the range of a Cray Y-MP8. We can probably go faster than a Y-MP8, but we don’t want to get too specific about it.”

M zero is not the only ultrapowerful silicon engine to gleam in the Chudnovskian oeuvre. The brothers recently fielded a supercomputer named Little Fermat, which they designed with Monty Denneau, an I.B.M. supercomputer architect, and Saed Younis, a graduate student at the Massachusetts Institute of Technology. Younis did the grunt work: he mapped out circuits containing more than fifteen thousand connections and personally plugged in some five thousand chips. Little Fermat is seven feet tall, and sits inside a steel frame in a laboratory at M.I.T., where it considers numbers.

What m zero consists of is a group of high-speed processors linked by cables (which cover the floor of the room). The cables form a network of connections among the processors—a web. Gregory sketched on a piece of paper the layout of the machine. He drew a box and put an “x” through it, to show the web, or network, and he attached some processors to the web:

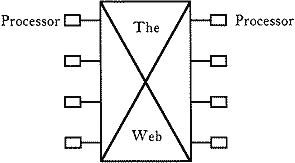
“Each processor is connected to a high-speed switching network that connects it to all the others,” he said. “It’s like a telephone network—everybody is talking to everybody else. As far as I know, no one except us has built a machine that has this type of web. In other parallel machines, the processors are connected only to near neighbors, while they have to talk to more distant processors through intervening processors. Think of a phone system: it wouldn’t be very pleasant if you had to talk to distant people by sending them messages through your neighbors. But the truth is that nobody really knows how the hell parallel machines should perform, or the best design for them. Right now we have eight processors. We plan to have two hundred and fifty-six processors. We will be able to fit them into the apartment.”

He said that each processor had its own memory attached to it, so that each processor was in fact a separate computer. After a processor was fed some data and had got a result, it could send the result through the web to another processor. The brothers wrote the machine’s application software in fortran, a programming language that is “a dinosaur from the late fifties,” Gregory said, adding, “There is always new life in this dinosaur.” The software can break a problem into pieces, sending the pieces to the machine’s different processors. “It’s the principle of divide and conquer,” Gregory said. He said that it was very hard to know what exactly was happening in the web when the machine was running—that the web seemed to have a life of its own.

“Our machine is mostly made of connections,” David said. “About ninety per cent of its volume is cables. Your brain is the same way. It is mostly made of connections. If I may say so, your brain is a liquid-cooled parallel supercomputer.” He pointed to his nose. “This is the fan.”

The design of the web is the key element in the Chudnovskian architecture. Behind the web hide several new findings in number theory, which the Chudnovskys have not yet published. The brothers would not disclose to me the exact shape of the web, or the discoveries behind it, claiming that they needed to protect their competitive edge in a worldwide race to develop faster supercomputers. “Anyone with a hundred million dollars and brains could be our competitor,” David said dryly.

The Chudnovskys have formidable competitors. Thinking Machines Corporation, in Cambridge, Massachusetts, sells massively parallel supercomputers. The price of the latest model, the CM-5, starts at one million four hundred thousand dollars and goes up from there. If you had a hundred million dollars, you could order a CM-5 that would be an array of black monoliths the size of a Burger King, and it would burn enough electricity to light up a neighborhood. Seymour Cray is another competitor of the brothers, as it were. He invented the original Cray series of supercomputers, and is now the head of the Cray Computer Corporation, a spinoff from Cray Research. Seymour Cray has been working to develop his Cray 3 for several years. His company’s effort has recently been troubled by engineering delays and defections of potential customers, but if the machine ever is released to customers it may be an octagon about four feet tall and four feet across, and it will burn more than two hundred thousand watts. It would melt instantly if its cooling system were to fail.

Then, there’s the Intel Corporation. Intel, together with a consortium of federal agencies, has invested more than twenty-seven million dollars in the Touchstone Delta, a five-foot-high, fifteen-foot-long parallel supercomputer that sits in a computer room at Caltech. The machine consumes twenty-five thousand watts of power, and is kept from overheating by chilled air flowing through its core. One day, I called Paul Messina, a Caltech research scientist, who is the head of the Touchstone Delta project, to get his opinion of the Chudnovsky brothers. It turned out that Messina hadn’t heard of them. As for their claim to have built a pi-computing gigaflop supercomputer out of mail-order parts for around seventy thousand dollars, he flatly believed it. “It can be done, definitely,” Messina said. “Of course, seventy thousand dollars is just the cost of the components. The Chudnovskys are counting very little of their human time.”

Yasumasa Kanada, the brothers’ pi rival at Tokyo University, uses a Hitachi S-820/80 supercomputer that is believed to be considerably faster than a Cray Y-MP8, and it burns close to half a million watts—half a megawatt, practically enough power to melt steel. The Chudnovsky brothers particularly hoped to leave Kanada and his Hitachi in the dust with their mail-order funny car.

“We want to test our hardware,” Gregory said.

“Pi is the best stress test for a supercomputer,” David said.

“We also want to find out what makes pi different from other numbers. It’s a business.”

“Galileo saw the moons of Jupiter through his telescope, and he tried to figure out the laws of gravity by looking at the moons, but he couldn’t,” David said. “With pi, we are at the stage of looking at the moons of Jupiter.” He pulled his Mini Mag-Lite flashlight out of his pocket and shone it into a bookshelf, rooted through some file folders, and handed me a color photograph of pi. “This is a piscape,” he said. The photograph showed a mountain range in cyberspace: bony peaks and ridges cut by valleys. The mountains and valleys were splashed with colors—yellow, green, orange, violet, and blue. It was the first eight million digits of pi, mapped as a fractal landscape by an I.B.M. GF-11 supercomputer at Yorktown Heights, which Gregory had programmed from his bed. Apart from its vivid colors, pi looks like the Himalayas.

Gregory thought that the mountains of pi seemed to contain structure. “I see something systematic in this landscape, but it may be just an attempt by the brain to translate some random visual pattern into order,” he said. As he gazed into the nature beyond nature, he wondered if he stood close to a revelation about the circle and its diameter. “Any very high hill in this picture, or any flat plateau, or deep valley, would be a sign of something in pi,” he said. “There are slight variations from randomness in this landscape. There are fewer peaks and valleys than you would expect if pi were truly random, and the peaks and valleys tend to stay high or low a little longer than you’d expect.” In a manner of speaking, the mountains of pi looked to him as if they’d been molded by the hand of the Nameless One, Deus absconditus (the hidden God), but he couldn’t really express in words what he thought he saw and, to his great frustration, he couldn’t express it in the language of mathematics, either.

“Exploring pi is like exploring the universe,” David remarked.

“It’s more like exploring underwater,” Gregory said. “You are in the mud, and everything looks the same. You need a flashlight. Our computer is the flashlight.”

David said, “Gregory—I think, really—you are getting tired.”

A fax machine in a corner beeped and emitted paper. It was a message from a hardware dealer in Atlanta. David tore off the paper and stared at it. “They didn’t ship it! I’m going to kill them! This a service economy. Of course, you know what that means— the service is terrible.”

“We collect price quotes by fax,” Gregory said.

“It’s a horrible thing. Window-shopping in supercomputerland. We can’t buy everything—”

“Because everything won’t exist,” Gregory said.

“We only want to build a machine to compute a few transcendental numbers—”

“Because we are not licensed for transcendental meditation,” Gregory said.

“Look, we are getting nutty,” David said.

“We are not the only ones,” Gregory said. “We are getting an average of one letter a month from someone or other who is trying to prove Fermat’s Last Theorem.

I asked the brothers if they had published any of their digits of pi in a book.

Gregory said that he didn’t know how many trees you would have to grind up in order to publish a billion digits of pi in a book. The brothers’ pi had been published on fifteen hundred microfiche cards stored somewhere in Gregory’s apartment. The cards held three hundred thousand pages of data, a slug of information much bigger than the Encylopaedia Britannica, and containing but one entry, “Pi.” David offered to find the cards for me; they had to be around here somewhere. He switched on the lights in the hallway and began to shift boxes. Gregory rifled bookshelves.

“Please sit down, Gregory,” David said. Finally, the brothers confessed that they had temporarily lost their pi. “Look, it’s not a problem,” David said. “We keep it in different places.” He reached inside m zero and pulled out a metal box. It was a naked hard-disk drive, studded with chips. He handed me the object. “There’s pi stored on this drive.” It hummed gently. “You are holding some pi in your hand. It weighs six pounds.”

Months passed before I visited the Chudnovskys again. The brothers had been tinkering with their machine and getting it ready to go for two billion digits of pi, when Gregory developed an abnormally related to one of his kidneys. He went to the hospital and had some cat scans made of his torso, to see what things looked like, but the brothers were disappointed in the pictures, and persuaded the doctors to give them the cat data on a magnetic tape. They took the tape home, processed it in m zero, and got spectacular color images of Gregory’s torso. The images showed cross-sectional slices of his body, viewed through different angles, and they were far more detailed than any image from a cat scanner. Gregory wrote the imaging software. It took him a few weeks. “There’s a lot of interesting mathematics in the problem of imaging a body,” he remarked. For the moment, it was more interesting than pi, and it delayed the brothers’ probe into the Ludolphian number.

Spring came, and Federal Express was active at the Chudnovskys’ building. Then the brothers began to calculate pi, slowly at first, more intensely as they gained confidence in their machine, but in May the weather warmed up and Con Edison betrayed the brothers. A heat wave caused a brownout in New York City, and as it struck, m zero automatically shut itself down, to protect its circuits, and died. Afterward, the brothers couldn’t get electricity running properly through the machine. They spent two weeks restarting it, piece by piece.

Then, on Memorial Day weekend, as the calculation was beginning to progress, Malka Benjaminovna suffered a heart attack. Gregory was alone with his mother in the apartment. He gave her chest compressions and breathed air into her lungs, although David later couldn’t understand how his brother didn’t kill himself saving her. An ambulance rushed her to St. Luke’s Hospital. The brothers were terrified that they would lose her, and the strain almost killed David. One day, he fainted in his mother’s hospital room and threw up blood. He had developed a bleeding ulcer. “Look, it’s not a problem,” he said later. After Malka Benjaminovna had been moved out of intensive care, Gregory rented a laptop computer, plugged it into the telephone line in her hospital room, and talked to m zero at night through cyberspace, driving the supercomputer toward pi and watching his mother’s blood pressure at the same time.

Malka Benjaminovna improved slowly. When St. Luke’s released her, the brothers settled her in her room in Gregory’s apartment and hired a nurse to look after her. I visited them shortly after that, on a hot day in early summer. David answered the door. There were blue half circles under his eyes, and he had lost weight. He smiled weakly and greeted me by saying, “I believe it was Oliver Heaviside, the English physicist, who once said, ‘In order to know soup, it is not necessary to climb into a pot and be boiled.’ But, look, if you want to be boiled you are welcome to come inside.” He led me down the dark hallway. Malka Benjaminovna was asleep in her bedroom, and the nurse was sitting beside her. Her room was lined with bookshelves, packed with paper—it was an overflow repository.

“Theoretically, the best way to cool a supercomputer is to submerge it in water,” Gregory said, from his bed in the junk yard.

“Then we could add goldfish,” David said.

“That would solve all our problems.”

“We are not good plumbers, Gregory. As long as I am alive, we will not cool a machine with water.”

“What is the temperature in there?” Gregory asked, nodding toward m zero’s room.

“It grows to thirty-four degrees Celsius. Above ninety Fahrenheit. This is not good. Things begin to fry.”

David took Gregory under the arm, and we passed through the French door into gloom and pestilential heat. The shades were drawn, the lights were off, and an air-conditioner in a window ran in vain. Sweat immediately began to pour down my body. “I don’t like to go into this room,” Gregory said. The steel frame in the center of the room—the heart of m zero—had acquired more logic boards, and more red lights blinked inside the machine. I could hear disk drives murmuring. The drives were copying and recopying segments of transcendental numbers, to check the digits for perfect accuracy. Gregory knelt on the floor, facing the steel frame.

David opened a cardboard box and removed an electronic board. He began to fit it into m zero. I noticed thathis hands were marked with small cuts, which he had got from reaching inside the machine.

“David, could you give me the flashlight?” Gregory said.

David pulled the Mini Mag-Lite from his shirt pocket and handed it to Gregory. The brothers knelt beside each other, Gregory shining the flashlight into the supercomputer. David reached inside with his fingers and palpated a logic board.

“Don’t!” Gregory said. “O.K., look. No! No!” They muttered to each other in Russian. “It’s too small,” Gregory said.

David adjusted an electric fan. “We bought it at a hardware store down the street,” he said to me. “We buy our fans in the winter. It saves money.” He pointed to a gauge that had a dial on it. “Here we have a meat thermometer.”

The brothers had thrust the thermometer between two circuit boards in order to look for hot spots inside m zero. The thermometer’s dial was marked “Beef Rare—Ham—Beef Med— Pork.”

“You want to keep the machine below ‘Pork,’ ” Gregory remarked. He lifted a keyboard out of the steel frame and typed something on it, staring at a display screen. Numbers filled the screen. “The machine is checking its memory,” he said. A buzzer sounded. “It shut down!” he said. “It’s a disk-drive controller. The stupid thing I obviously has problems.”

“It’s mentally deficient,” David commented. He went over to a bookshelf and picked up a hunting knife. I thought he was going to plunge it into the supercomputer, but he used it to rip open a cardboard box. “We’re going to ship the part back to the manufacturer,” he said to me. “You had better send it in the original box or you may not get your money back. Now you know the reason this apartment is full of empty boxes. We have to save them. Gregory, I wonder if you are tired.”

“If I stand up now, I will fall down,” Gregory said, from the floor. “Therefore, I will sit in my center of gravity. I will maintain my center of gravity. Let me see, meanwhile, what is happening with this machine.” He typed something on his keyboard. “You won’t believe it, Dave, but the controller now seems to work.”

“We need to buy a new one,” David said.

“Try Nevada.”

David dialled a mail-order house in Nevada that here will be called Searchlight Computers. He said loudly, in a thick Russian accent, “Hi, Searchlight.

I need a fifteen-forty controller. . . . No! No! No! I don’t need anything else! Just the controller! Just a naked unit! Naked! How much you charge?. . . Two hundred and fifty-seven dollars?”

Gregory glanced at his brother and shrugged. “Eh.”

“Look, Searchlight, can you ship it to me Federal Express? For tomorrow morning. How much?. . . Thirty-nine dollars for Fed Ex? Come on! What about afternoon delivery? . . . Twenty-nine dollars before 3p.m.? Relax. What is your name?. . . Bob. Fine. O.K. So it’s two hundred and fifty- seven dollars plus twenty-nine dollars for Federal Express?”

“Twenty-nine dollars for Fed Ex!” Gregory burst out. “It should be fifteen.” He pulled a second keyboard out of the steel frame and tapped the keys. Another display screen came alive and filled with numbers.

“Tell me this,” David said to Bob in Nevada. “Do you have thirty-day money-back guarantee? . . . No? Come on! Look, any device might not work.”

“Of course, a part might work,” Gregory muttered to his brother. “But it usually doesn’t.”

“Question Number Two: The Fed Ex should not cost twenty-nine bucks,” David said to Bob. “No? nothing! I’m just asking.” David hung up the phone. “I’m going to call A.K.,” he said. “Hi, A.K., this is David Chudnovsky, calling from New York. A.K., I needanother controller, like the one you sent. Can you send it today Fed Ex?. . . How much you charge?. . . Naked! I want a naked unit! Not in a shoebox, nothing!”

A rhythmic clicking sound came from one of the disk drives. Gregory remarked to me, “We are calculating pi right now.”

“Do you want my MasterCard? Look, it’s really imperative that I get my unit tomorrow. A.K., please, I really need my unit bad.” David hung up the telephone and sighed. “This is what has happened to a pure mathematician.”

"Gregory and David are both extremely childlike, but I don’t mean childish at all,” Gregory’s wife, Christine Pardo Chudnovsky, said one muggy summer day, at the dining-room table. “There is a certain amount of play in everything they do, a certain amount of fooling around between two brothers.” She is six years younger than Gregory; she was an undergraduate at Barnard College when she first met him. “I fell in love with Gregory immediately. His illness came with the package.” She is still in love with him, even if at times they fight over his heaps of paper. (“I don’t have room to put my things down,” she says to him.) As we talked, though, pyramids of boxes and stacks of paper leaned against the dining-room windows, pressing against the glass and blocking daylight, and a smell of hot electrical gear crept through the room. “This house is an example of mathematics in family life,” she said. At night, she dreams that she is dancing from room to room through an empty apartment that has parquet floors.

David brought his mother out of her bedroom, settled her at the table, and kissed her on the cheek. Malka Benjaminovna seemed frail but alert. She is a small, white-haired woman with a fresh face and clear blue eyes, who speaks limited English. A mathematician once described Malka Benjaminovna as the glue that holds the Chudnovsky family together. She was an engineer during the Second World War, when she designed buildings, laboratories, and proving grounds in the Urals for testing the Katyusha rocket; later, she taught engineering at schools around Kiev. She handed me plates of roast chicken, kasha, pickles, cream cheese, brown bread, and little wedges of The Laughing Cow cheese in foil. “Mother thinks you aren’t getting enough to eat,” Christine said. Malka Benjaminovna slid a jug of Gatorade across the table at me.

After lunch, and fortified with Gatorade, the brothers and I went into the chamber of m zero, into a pool of thick heat. The room enveloped us like noon on the Amazon, and it teemed with hidden activity. The disk drives clicked, the red lights flashed, the air-conditioner hummed, and you could hear dozens of whispering fans. Gregory leaned on his cane and contemplated the machine. “It’s doing many jobs et the moment,” he said. “Frankly, I don’t know what it’s doing. It’s doing some algebra, and I think it’s also backing up some pieces of pi.”

“Sit down, Gregory, or you will fall,” David said.

“What is it doing now, Dave?”

“It’s blinking.”

“It will die soon.”

“Gregory, I heard a funny noise.”

“You really heard it? Oh, God, it’s going to be like the last time—”

“That’s it!”

“We are dead! It crashed!”

“Sit down, Gregory, for God’s sake!”

Gregory sat on a stool and tugged at his beard. “What was I doing before the system crashed? With God’s help, I will remember.” He jotted a few notes in a laboratory notebook. David slashed open a cardboard box with his hunting knife and lifted out a board studded with chips, for making color images on a display screen, and plugged it into m zero. Gregory crawled under a table. “Oh, shit,” he said, from beneath the table.

“Gregory, you killed the system again!”

“Dave, Dave, can you get me a flashlight?”

David handed his Mini Mag-Lite under the table. Gregory joined some cables together and stood up. “Whoo! Very uncomfortable. David, boot it up.”

“Sit down for a moment.”

Gregory slumped into a chair.

“This monster is going on the blink,” David said, tapping a keyboard.

“It will be all right.”

On a screen, m zero declared, “The system is ready.”

“Ah,” David said.

The drives began to click, and the parallel processors silently multiplied and conjoined huge numbers. Gregory headed for bed, David holding him by the arm.

In the junk yard, his nest, his paper-lined oubliette, Gregory kicked off hi gentleman’s slippers, lay down on the bed, and predicted the future. He said “The gigaflop supercomputers of today are almost useless. What is needed is a teraflop machine. That’s a machine that can run at a trillion flops, a trillion floating-point operations per second, or roughly a thousand times as fast as Cray Y-MP8. One such design for teraflop machine, by Monty Denneau at I.B.M., will be a parallel supercomputer in the form of a twelve-foot wide box. You want to have at least sixty-four thousand processors in the machine, each of which has the power of a Cray. And the processors will be joined by a network that has the total switching capacity of the entire telephone network in the United States. I think a teraflop machine will exist by 1993. Now, a better machine is a petaflop machine. A petaflop is a quadrillion flops, a quadrillion floating-point operations per second, so a petaflop machine is a thousand times as fast as a teraflop machine, or a million times as fast as a Cray Y-MP8. The petaflop machine will exist by the year 2000, or soon afterward. It will fit into a sphere less than a hundred feet in diameter. It will use light and mirrors—the machine’s network will consist of optical cables rather than copper wires. By that time, a gigaflop ‘supercomputer’ will be a single chip. I think that the petaflop machine will be used mainly to simulate machines like itself, so that we can begin to design some real machines.”

In the nineteenth century, mathematicians attacked pi with the help of human computers. The most powerful of these was Johann Martin Zacharias Dase, a prodigy from Hamburg. Dase could multiply large numbers in his head, and he made a living exhibiting himself to crowds in Germany, Denmark, and England, and hiring himself out to mathematicians. A mathematician once asked Dase to multiply 79,532,853 by 93,758,479, and Dase gave the right answer in fifty-four seconds. Dase extracted the square root of a hundred-digit number in fifty-two minutes, and he was able to multiply a couple of hundred-digit numbers in his head during a period of eight and three-quarters hours. Dase could do this kind of thing for weeks on end, running as an unattended supercomputer. He would break off a calculation at bedtime, store everything in his memory for the night, and resume calculation in the morning. Occasionally, Dase had a system crash. In 1845, he bombed while trying to demonstrate his powers to a mathematician and astronomer named Heinrich Christian Schumacher, reckoning wrongly every multiplication that he attempted. He explained to Schumacher that he had a headache. Schumacher also noted that Dase did not in the least understand theoretical mathematics. A mathematician named Julius Petersen once tried in vain for six weeks to teach Dase the rudiments of Euclidean geometry, but they absolutely baffled Dase. Large numbers Dase could handle, and in 1844 L. K. Schulz von Strassnitsky hired him to compute pi. Dase ran the job for almost two months in his brain, and at the end of the time he wrote down pi correctly to the first two hundred decimal places— then a world record.

To many mathematicians, mathematical objects such as the number pi seem to exist in an external, objective reality. Numbers seem to exist apart from time or the world; numbers seem to transcend the universe; numbers might exist even if the universe did not. I suspect that in their hearts most working mathematicians are Platonists, in that they take it as a matter of unassailable if unprovable fact that mathematical reality stands apart from the world, and is at least as real as the world, and possibly gives shape to the world, as Plato suggested. Most mathematicians would probably agree that the ratio of the circle to its diameter exists brilliantly in the nature beyond nature, and would exist even if the human mind was not aware of it, and might exist even if God had not bothered to create it. One could imagine that pi existed before the universe came into being and will exist after the universe is gone. Pi may even exist apart from God, in the opinion of some mathematicians, for while there is reason to doubt the existence of God, by their way of thinking there is no good reason to doubt the existence of the circle.

“To an extent, pi is more real than the machine that is computing it,” Gregory remarked to me one day. “Pinto was right. I am a Platonist. Of course pi is a natural object. Since pi is there, it exists. What we are doing is really close to experimental physics—we are ‘observing pi.’ Since we can observe pi, I prefer to think of pi as a natural object. Observing pi is easier than studying physical phenomena, because you can prove things in mathematics, whereas you can’t prove anything in physics. And, unfortunately, the laws of physics change once every generation.”

“Is mathematics a form of art?” I asked.

“Mathematics is partially an art, even though it is a natural science,” he said. “Everything in mathematics does exist now. It’s a matter of naming it. The thing doesn’t arrive from God in a fixed form; it’s a matter of representing it with symbols. You put it through your mind in order to make sense of it.”

Mathematicians have sorted numbers into classes in order to make sense of them. One class of numbers is that of the rational numbers. A rational number is a fraction composed of integers (whole numbers): 1/1, 1/3, 3/5, 10/71, and so on. Every rational number, when it is expressed in decimal form, repeats periodically: 1/3, for example, becomes .333. . . . Next, we come to the irrational numbers. An irrational number can’t be expressed as a fraction composed of whole numbers, and, furthermore, its digits go to infinity without repeating periodically.

The square root of two (√2) is an irrational number. There is simply no way to represent any irrational number as the ratio of two whole numbers; it can’t be done. Hippasus of Metapontum supposedly made this discovery in the fifth century B.C., while travelling in a boat with some mathematicians who were followers of Pythagoras. The Pythagoreans believed that everything in nature could be reduced to a ratio of two whole numbers, and they threw Hippasus overboard for his discovery, since he had wrecked their universe. Expanded as a decimal, the square root of two begins 1.41421 . . . and runs in “random” digits forever. It looks exactly like pi in its decimal expansion; it is a hopeless jumble, showing no obvious system or design. The square root of two is not a transcendental number, because it can be found with an equation. It is the solution (root) of an equation. The equation is x2 = 2, and a solution is the square root of two. Such numbers are called algebraic.

While pi is indeed an irrational number—it can’t be expressed as a fraction made of whole numbers—more important, it can’t be expressedwith finite algebra. Pi is therefore said to be a transcendental number, because it transcends algebra. Simply and generally speaking, a transcendental number can’t be pinpointed through an equation built from a finite number of integers. There is no finite algebraic equation built from whole numbers that will give an exact value for pi. The statement can be turned around this way: pi is not the solution to any equation built from a less than infinite series of whole numbers. If equations are trains threading the landscape of numbers, then no train stops at pi.

Pi is elusive, and can be approached only through rational approximations. The approximations hover around the number, closing in on it, but do not touch it. Any formula that heads toward pi will consist of a chain of operations that never ends. It is an infinite series. In 1674, Gottfried Wilhelm Leibniz (the co-inventor of the calculus, along with Isaac Newton) noticed an extraordinary pattern of numbers buried in the circle. The Leibniz series for pi has been called one of the most beautiful mathematical discoveries of the seventeenth century:

?/4 = 1/1 - 1/3 + 1/5 -1/7 + 1/9 - . . . .

In English: pi over four equals one minus a third plus a fifth minus a seventh plus a ninth—and so on. You follow the odd numbers out to infinity, and when you arrive there and sum the terms, you get pi. But since you never arrive at infinity you never get pi. Mathematicians find it deeply mysterious that a chain of discrete rational numbers can connect so easily to geometry, to the smooth and continuous circle.

As an experiment in “observing pi,” as Gregory Chudnovsky puts it, I computed the Leibniz series on a pocket calculator. It was easy, and I got results that did seem to wander slowly toward pi. As the series progresses, the answers touch on 2.66, 3.46, 2.89, and 3.34, in that order. The answers land higher than pi and lower than pi, skipping back and forth across pi, and gradually closing in on pi. A mathematician would say that the series “converges on pi.” It converges on pi forever, playing hopscotch over pi but never landing on pi.

You can take the Leibniz series out a long distance—you can even dramatically speed up its movement toward pi by adding a few corrections to it—but no matter how far you take the Leibniz series, and no matter how many corrections you hammer into it, when you stop the operation and sum the terms, you will get a rational number that is somewhere around pi but is not pi, and you will be damned if you can put your hands on pi.

Transcendental numbers continue forever, as an endless non-repeating string, in whatever rational form you choose to display them, whether as digits or as an equation. The Leibniz series is a beautiful way to represent pi, and it is finally mysterious, because it doesn’t tell us much about pi. Looking at the Leibniz series, you feel the independence of mathematics from human culture. Surely, on any world that knows pi the Leibniz series will also be known. Leibniz wasn’t the first mathematician to discover the Leibniz series. Nilakantha, an astronomer, grammarian, and mathematician who lived on the Kerala coast of India, described the formula in Sanskrit poetry around the year 1500.

It is worth thinking about what a decimal place means. Each decimal place of pi is a range that shows the approximate location of pi to an accuracy ten times as great as the previous range. But as you compute the next decimal place you have no idea where pi will appear in the range. It could pop up in 3, or just as easily in 9, or in 2. The apparent movement of pi as you narrow the range is known as the random walk of pi.

Pi does not move; pi is a fixed point. The algebra wobbles around pi. There is no such thing as a formula that is steady enough or sharp enough to stick a pin into pi. Mathematicians have discovered formulas that converge on pi very fast (that is, they skip around pi with rapidly increasing accuracy), but they do not and cannot hit pi. The Chudnovsky brothers discovered their own formula in 1984, and it attacks pi with great ferocity and elegance. The Chudnovsky formula is the fastest series for pi ever found which uses rational numbers. Various other series for pi, which use irrational numbers, have also been found, and they converge on pi faster than the Chudnovsky formula, but in practice they run more slowly on a computer, because irrational numbers are harder to compute. The Chudnovsky formula for pi is thought to be “extremely beautiful,’ by persons who have a good feel for numbers, and it is based on a torus (a doughnut), rather than on a circle. It uses large assemblages of whole numbers to hunt for pi, and it owes much to an earlier formula for pi worked out in 1914 by Srinivasa Ramanujan, a mathematician from Madras, who was a number theorist of unsurpassed genius. Gregory says that the Chudnovsky formula “is in the style of Ramanujan,” and that it “is really very simple, and can be programmed into a computer with a few lines of code.”

In 1873, Georg Cantor, a Russian-born mathematician who was one of the towering intellectual figures of the nineteenth century, proved that the set of transcendental numbers is infinitely more extensive than the set of algebraic numbers. That is, finite algebra can’t find or describe most numbers. To put it another way, most numbers are infinitely long and non-repeating in any rational form of representation. In this respect, most numbers are like pi.

Cantor’s proof was a disturbing piece of news, for at that time very few transcendental numbers were actually known. (Not until nearly a decade later did Ferdinand Lindemann finally prove the transcendence of pi; before that, mathematicians had only conjectured that pi was transcendental.) Perhaps even more disturbing, Cantor offered no clue, in his proof, to what a transcendental number might look like, or how to construct such a beast. Cantor’s celebrated proof of the existence of uncountable multitudes of transcendental numbers resembled a proof that the world is packed with microscopic angels—a proof, however, that does not tell us what the angels look like or where they can be found; it merely proves that they exist in uncountable multitudes. While Cantor’s proof lacked any specific description of a transcendental number, it showed that algebraic numbers (such as the square root of two) are few and far between: they poke up like marker buoys through the sea of transcendental numbers.

Cantor’s proof disturbed some mathematicians because, in the first place, it suggested that they had not yet discovered most numbers, which were transcendentals, and in the second place that they lacked any tools or methods that would determine whether a given number was transcendental or not. Leopold Kronecker, an influential older mathematician, rejected Cantor’s proof, and resisted the whole notion of “discovering” a number. (He once said, in a famous remark, “God made the integers, all else is the work of man.”) Cantor’s proof has withstood such attacks, and today the debate over whether transcendental numbers are a work of God or man has subsided, mathematicians having decided to work with transcendental numbers no matter who made them.

The Chudnovsky brothers claim that the digits of pi form the most nearly perfect random sequence of digits that has ever been discovered. They say that nothing known to humanity appears to be more deeply unpredictable than the succession of digits in pi, except, perhaps, the haphazard clicks of a Geiger counter as it detects the decay of radioactive nuclei. But pi is not random. The fact that pi can be produced by a relatively simple formula means that pi is orderly. Pi looks random only because the pattern in the digits is fantastically complex. The Ludolphian number is fixed in eternity—not a digit out of place, all characters in their proper order, an endless sentence written to the end of the world by the division of the circle’s diameter into its circumference. Various simple methods of approximation will always yield the same succession of digits in the same order. If a single digit in pi were to be changed anywhere between here and infinity, the resulting number would no longer be pi; it would be “garbage,” in David’s word, because to change a single digit in pi is to throw all the following digits out of whack and miles from pi.

“Pi is a damned good fake of a random number,” Gregory said. “I just wish it were not as good a fake. It would make our lives a lot easier.”

Around the three-hundred-millionth decimal place of pi, the digits go 88888888—eight eights pop up in a row. Does this mean anything? It appears to be random noise. Later, ten sixes erupt: 6666666666. What does this mean? Apparently nothing, only more noise. Somewhere past the half-billion mark appears the string 123456789. It’s an accident, as it were. “We do not have a good, clear, crystallized idea of randomness,” Gregory said. “It cannot be that pi is truly random. Actually, a truly random sequence of numbers has not yet been discovered.”

No one knows what happens to the digits of pi in the deeper regions, as the number is resolved toward infinity. Do the digits turn into nothing but eights and fives, say? Do they show a predominance of sevens? Similarly, no one knows if a digit stops appearing in pi. This conjecture says that after a certain point in the sequence a digit drops out completely. For example, no more fives appear in pi—something like that. Almost certainly, pi does not do such things, Gregory Chudnovsky thinks, because it would be stupid, and nature isn’t stupid. Nevertheless, no one has ever been able to prove or disprove a certain basic conjecture about pi: that every digit has an equal chance of appearing in pi. This is known as the normality conjecture for pi. The normality conjecture says that, on average, there is no more or less of any digit in pi: for example, there is no excess of sevens in pi. If all digits do appear with the same average frequency in pi, then pi is a “normal” number—“normal” by the narrow mathematical definition of the word. “This is the simplest possible conjecture about pi,” Gregory said. “There is absolutely no doubt that pi is a ‘normal’ number. Yet we can’t prove it. We don’t even know how to try to prove it. We know very little about transcendental numbers, and, what is worse, the number of conjectures about them isn’t growing.” No one knows even how to tell the difference between the square root of two and pi merely by looking at long strings of their digits, though the two numbers have completely distinct mathematical properties, one being algebraic and the other transcendental.

Even if the brothers couldn’t prove anything about the digits of pi, they felt that by looking at them through the window of their machine they might at least see something that could lead to an important conjecture about pi or about transcendental numbers as a class. You can learn a lot about all cats by looking closely at one of them. So if you wanted to look closely at pi how much of it could you see with a very large supercomputer? What if you turned the universe into a supercomputer? What then? How much pi could you see? Naturally, the brothers had considered this project. They had imagined a computer built from the universe. Here’s how they estimated the machine’s size. It has been calculated that there are about 1079 electrons and protons in the observable universe; this is the so-called Eddington number of the universe. (Sir Arthur Stanley Eddington, the astrophysicist, first came up with the number.) The Eddington number is the digit 1 followed by seventy-nine zeros: 10,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000. Ten vigintsextillion. The Eddington number. It declares the power of the Eddington machine.

The Eddington machine would be the universal supercomputer. It would be made of all the atoms in the universe. The Eddington machine would contain ten vigintsextillion parts, and if the Chudnovsky brothers could figure out how to program it with fortran they might make it churn toward pi. “In order to study the sequence of pi, you have to store it in the Eddington machine’s memory,” Gregory said. To be realistic, the brothers thought that a practical Eddington machine wouldn’t be able to store pi much beyond 1077 digits—a number that is only a hundredth of the Eddington number. Now, what if the digits of pi only begin to show regularity beyond 1077 digits? Suppose, for example, that pi manifests a regularity starting at 10100 decimal places? That number is known as a googol. If the design in pi appears only after a googol of digits, then not even the Eddington machine will see any system in pi; pi will look totally disordered to the universe, even if pi contains a slow, vast, delicate structure. A mere googol of pi might be only the first knot at the corner of a kind of limitless Persian rug, which is woven into increasingly elaborate diamonds, cross-stars, gardens, and cosmogonies. It may never be possible, in principle, to see the order in the digits of pi. Not even nature itself may know the nature of pi.

“If pi doesn’t show systematic behavior until more than ten to the seventy-seven decimal places, it would really be a disaster,” Gregory said. “It would be actually horrifying.”

“I wouldn’t give up,” David said. “There might be some other way of leaping over the barrier—”

“And of attacking the son of a bitch,” Gregory said.

The brothers first came in contact with the membrane that divides the dreamlike earth from mathematical reality when they were boys, growing up in Kiev, and their father gave David a book entitled “What Is Mathematics?,” by two mathematicians named Richard Courant and Herbert Robbins. The book is a classic—millions of copies of it have been printed in unauthorized Russian and Chinese editions alone—and after the brothers finished reading “Robbins,” as the book is called in Russia, David decided to become a mathematician, and Gregory soon followed his brother’s footsteps into the nature beyond nature. Gregory’s first publication, in the journal Soviet Mathematics—Doklady, came when he was sixteen years old: “Some Results in the Theory of Infinitely Long Expressions.” Already you can see where he was headed. David, sensing his younger brother’s power, encouraged him to grapple with central problems in mathematics. Gregory made his first major discovery at the age of seventeen, when he solved Hilbert’s Tenth Problem. (It was one of twenty-three great problems posed by David Hilbert in 1900.) To solve a Hilbert problem would be an achievement for a lifetime; Gregory was a high-school student who had read a few books on mathematics. Strangely, a young Russian mathematician named Yuri Matyasevich had just solved Hilbert’s Tenth Problem, and the brothers hadn’t heard the news. Matyasevich has recently said that the Chudnovsky method is the preferred way to solve Hilbert’s Tenth Problem.

The brothers enrolled at Kiev State University, and both graduated summa cum laude. They took their Ph.D.s at the Institute of Mathematics at the Ukrainian Academy of Sciences. At first, they published their papers separately, but by the mid-nineteen-seventies they were collaborating on much of their work. They lived with their parents in Kiev until the family decided to try to take Gregory abroad for treatment, and in 1976 Volf and Malka Chudnovsky applied to the government to emigrate. Volf was immediately fired from his job.

The K.G.B. began tailing the brothers. “Gregory would not believe me until it became totally obvious,” David said. “I had twelve K.G.B. agents on my tail. No, look, I’m not kidding! They shadowed me around the clock in two cars, six agents in each car. Three in the front seat and three in the back seat. That was how the K.G.B. operated.” One day, in 1976, David was walking down the street when K.G.B. officers attacked him, breaking his skull. He went home and nearly died, but didn’t go to the hospital. “If I had gone to the hospital, I would have died for sure,” he told me. “The hospital is run by the state. I would forget to breathe.”

On July 22, 1977, plainclothesmen from the K.G.B. accosted Volf and Malka on a street in Kiev and beat them up. They broke Malka’s arm and fractured her skull. David took his mother to the hospital. “The doctor in the emergency room said there was no fracture,” David said.

Gregory, at home in bed, was not so vulnerable. Also, he was conspicuous in the West. Edwin Hewitt, a mathematician at the University of Washington, in Seattle, had visited Kiev in 1976 and collaborated with Gregory on a paper, and later, when Hewitt learned that the Chudnovsky family was in trouble, he persuaded Senator Henry M. Jackson, the powerful member of the Senate Armed Services Committee, to take up the Chudnovskys’ case. Jackson put pressure on the Soviets to let the family leave the country. Just before the K.G.B. attacked the parents, two members of a French parliamentary delegation that was in Kiev made an unofficial visit to the Chudnovskys to see what was going on. One of the visitors, a staff member of the delegation, was Nicole Lannegrace, who married David in 1983. Andrei Sakharov also helped to draw attention to the Chudnovskys’ increasingly desperate situation. Two months after the parents were attacked, the Soviet government unexpectedly let the family go. “That summer when I was getting killed by the K.G.B., I could never have imagined that the next year I would be in Paris or that I would wind up in New York, married to a beautiful Frenchwoman,” David said.The Chudnovsky family settled in New York, near Columbia University.

If pi is truly random? then at times pi will appear to be ordered. Therefore, if pi is random it contains accidental order. For example, somewhere in pi a sequence may run 07070707070707 for as many decimal places as there are, say, hydrogen atoms in the sun. It’s just an accident. Somewhere else the same sequence of zeros and sevens may appear, only this time interrupted by a single occurrence of the digit 3. Another accident. Those and all other “accidental” arrangements of digits almost certainly erupt in pi, but their presence has never been proved. “Even if pi is not truly random, you can still assume that you get every string of digits in pi,” Gregory said.

If you were to assign letters of the alphabet to combinations of digits, and were to do this for all human alphabets, syllabaries, and ideograms, then you could fit any written character in any language to a combination of digits in pi. According to this system, pi could be turned into literature. Then, if you could look far enough into pi, you would probably find the expression “See the U.S.A. in a Chevrolet!” a billion times in a row. Elsewhere, you would find Christ’s Sermon on the Mount in His native Aramaic tongue, and you would find versions of the Sermon on the Mount that are pure blasphemy. Also, you would find a dictionary of Yanomamo curses. A guide to the pawnshops of Lubbock. The book about the sea which James Joyce supposedly declared he would write after he finished “Finnegans Wake.” The collected transcripts of “The Tonight Show” rendered into Etruscan. “Knowledge of All Existing Things,” by Ahmes the Egyptian scribe. Each occurrence of an apparently ordered string in pi, such as the words “Ruin hath taught me thus to ruminate / That Time will come and take my love away,” is followed by unimaginable deserts of babble. No book and none but the shortest poems will ever be seen in pi, since it is infinitesimally unlikely that even as brief a text as an English sonnet will appear in the first 1077 digits of pi, which is the longest piece of pi that can be calculated in this universe.

Anything that can be produced by a simple method is by definition orderly. Pi can be produced by various simple methods of rational approximation, and those methods yield the same digits in a fixed order forever. Therefore, pi is orderly in the extreme. Pi may also be a powerful random-number generator, spinning out any and all possible combinations of digits. We see that the distinction between chance and fixity dissolves in pi. The deep connection between disorder and order, between cacophony and harmony, in the most famous ratio in mathematics fascinated Gregory and David Chudnovsky. They wondered if the digits of pi had a personality.

“We are looking for the appearance of some rules that will distinguish the digits of pi from other numbers,” Gregory explained. “It’s like studying writers by studying their use of words, their grammar. If you see a Russian sentence that extends for a whole page, with hardly a comma, it is definitely Tolstoy. If someone were to give you a million digits from somewhere in pi, could you tell it was from pi? We don’t really look for patterns; we look for rules. Think of games for children. If I give you the sequence one, two, three, four, five, can you tell me what the next digit is? Even a child can do it; the next digit is six. How about this game? Three, one, four, one, five, nine. Just by looking at that sequence, can you tell me the next digit? What if I gave you a sequence of a million digits from pi? Could you tell me the next digit just by looking at the sequence? Why does pi look like a totally unpredictable sequence with the highest complexity? We need to find out the rules that govern this game. For all we know, we may never find a rule in pi.”

Herbert Robbins, the co-author of “What Is Mathematics?,” is an emeritus professor of mathematical statistics at Columbia University. For the past six years, he has been teaching at Rutgers. The Chudnovskys call him once in a while to get his advice on how to use statistical tools to search for signs of order in pi. Robbins lives in a rectilinear house that has a lot of glass in it, in the woods on the outskirts of Princeton. Some of the twentieth century’s most creative and powerful discoveries in statistics and probability theory happened inside his head. Robbins is a tall, restless man in his seventies, with a loud voice furrowed cheeks, and penetrating eyes One recent day, he stretched himself out on a daybed in a garden room in his house and played with a rubber band, making a harp across his fingertips.

“It is a very difficult philosophical question, the question of what ‘random’ is,” he said. He plucked the rubber band with his thumb, boink, boink. “Everyone knows the famous remark of Albert Einstein, that God does not throw dice. Einstein just would not believe that there is an element of randomness in the construction of the world. The question of whether the universe is a random process or is determined in some way is a basic philosophical question that has nothing to do with mathematics. The question is important. People consider it when they decide what to do with their lives. It concerns religion. It is the question of whether our fate will be revealed or whether we live by blind chance. My God, how many people have been murdered over an answer to that question! Mathematics is a lesser activity than religion in the sense that we’ve agreed not to kill each other but to discuss things.”

Robbins got up from the daybed and sat in an armchair. Then he stood up and paced the room, and sat at a table in the room, and sat on a couch, and went back to the table, and finally returned to the daybed. The man was in constant motion. It looked random to me, but it may have been systematic. It was the random walk of Herbert Robbins.

“Mathematics is broken into tiny specialties today, but Gregory Chudnovsky is a generalist who knows the whole of mathematics as well as anyone,” he said as he moved around. “You have to go back a hundred years, to David Hilbert, to find a mathematician as broadly knowledgeable as Gregory Chudnovsky. He’s like Mozart: he’s the last of his breed. I happen to think the brothers’ pi project is a will-o’-the-wisp, and is one of the least interesting things they’ve ever done. But what do I know? Gregory seems to be asking questions that can’t be answered. To ask for the system in pi is like asking ‘Is there life after death?’ When you die, you’ll find out. Most mathematicians are not interested in the digits of pi, because the question is of no practical importance. In order for a mathematician to become interested in a problem, there has to be a possibility of solving it. If you are an athlete, you ask yourself if you can jump thirty feet. Gregory likes to ask if he can jump around the world. He likes to do things that are impossible.”

At some point after the brothers settled in New York, it became obvious that Columbia University was not going to be able to invite them to become full-fledged members of the faculty. Since then, the brothers have always enjoyed cordial personal relationships with various members of the faculty, but as an institution the Mathematics Department has been unable to create permanent faculty positions for them. Robbins and a couple of fellow-mathematicians—Lipman Bers and the late Mark Kac—once tried to raise money from private sources for an endowed chair at Columbia to be shared by the brothers, but the effort failed. Then the John D. and Catherine T. MacArthur Foundation awarded Gregory Chudnovsky a “genius” fellowship; that happened in 1981, the first year the awards were given, as if to suggest that Gregory is a person for whom the MacArthur prize was invented. The brothers can exhibit other fashionable paper—a Prix Peccot-Vimont, a couple of Guggenheims, a Doctor of Science honoris causa from Bard College, the Moscow Mathematical Society Prize—but there is one defect in their résumé, which is the fact that Gregory has to lie in bed most of the day. The ugly truth is that Gregory Chudnovsky can’t get a permanent job at any American institution of higher learning because he is physically disabled. But there are other, more perplexing reasons that have led the Chudnovsky brothers to pursue their work in solitude, outside the normal academic hierarchy, since the day they arrived in the United States.

Columbia University has awarded each brother the title of senior research scientist in the Department of Mathematics. Their position at Columbia is ambiguous. The university officially considers them to be members of the faculty, but they don’t have tenure, and Columbia doesn’t spend its own funds to pay their salaries or to support their research. However, Columbia does give them health-insurance benefits and a housing subsidy.

The brothers have been living on modest grants from the National Science Foundation and various other research agencies, which are funnelled through Columbia and have to be applied for regularly. Nicole Lannegrace and Christine Chudnovsky financed m zero out of their paychecks. Christine’s father, Gonzalo Pardo, who is a professor of dentistry at the State University of New York at Stony Brook, built the steel frame for m zero in his basement during a few weekends, using a wrench and a hacksaw.

The brothers’ mode of existence has come to be known among mathematicians as the Chudnovsky Problem. Herbert Robbins eventually decided that it was time to ask the entire American mathematics profession why it could not solve the Chudnovsky Problem. Robbins is a member of the National Academy of Sciences, and in 1986 he sent a letter to all of the mathematicians in the academy:

I fear that unless a decent and honorable position in the American educational and research system is found for the brothers soon, a personal and scientific tragedy will take place for which all American mathematicians will share responsibility. . . .
I have asked many of my colleagues why this situation exists, and what can be done to put an end to what I regard as a national disgrace. I have never received an answer that satisfies me.... I am asking you, then, as one of the leaders of American mathematics, to tell me what you are prepared to do to acquaint yourselves with their present circumstances, and if you are convinced of the merits of their case, to find a suitable position somewhere in the country for them as a pair.

There wasn’t much of a response. Robbins says that he received three written replies to his letter. One, from a faculty member at a well-known East Coast university, complained about David Chudnovsky’s personality. He remarked that “when David learns to be less overbearing” the brothers might have better luck. He also did not fully understand the tone of Robbins’ letter: while he agreed that some resolution to the Chudnovsky Problem must be found, he thought that Herb Robbins ought to approach the subject realistically and with more candor. (“More candor? How could I have been more candid?” Robbins asked.) Another letter came from a faculty member at Princeton University, who offered to put in a good word with the National Science Foundation to help the brothers get their grants, but did not mention a job at Princeton or anywhere else. The most thoughtful response came from a faculty member at M.I.T., who remarked, “It does seem odd that they have not been more sought after.” He wondered if in some part this might be a consequence of their breadth. “A specialist appears as a safer investment to a cautious academic administrator. I’m sorry I have nothing more effective to propose.”

An emotional reaction to Robbins’ campaign on behalf of the Chudnovskys came a bit later from Edwin Hewitt, the mathematician who had helped get the family out of the Soviet Union, and one of the few Americans who has ever worked with Gregory Chudnovsky. Hewitt wrote to colleagues, “I have collaborated with many excellent mathematicians . . . but with no one else have I witnessed an outpouring of mathematics like that from Gregory. He simply knows what is true and what is not.” In another letter, Hewitt wrote:

The Chudnovsky situation is a national disgrace. Everyone says, “Oh, what a crying shame” & then suggests that they be placed at somebody else’s institution. No one seems to want the admittedly burdensome task of caring for the Chudnovsky family. I imagine it would be a full-time, if not an impossible, job. We may remember that both Mozart and Beethoven were disagreeable people, to say nothing of Gauss.

The brothers would have to be hired as a pair. Gregory won’t take any job unless David gets one, and vice versa. Physically and intellectually commingled, like two trees that have grown together at the root and bole, the brothers claim that they can’t be separated without becoming deadfalls and crashing to the ground. To hire the Chudnovsky pair, a department would have to create a joint opening for them. Gregory can’t teach classes in the normal way, because he is more or less confined to bed. It would require a small degree of flexibility in a department to allow Gregory to concentrate on research, while David handled the teaching. The problem is that Gregory might still have the pleasure of working with a few brilliant graduate students—a privilege that might not go down well in an American academic department.

“They are prototypical Russians,” Robbins said. “They combine a rather grandiose vision of themselves with an ability to live on scraps rather than compromise their principles. These are people the world is not able to cope with, and they are not making it any easier for the world. I don’t see that the world is particularly trying to keep Gregory Chudnovsky alive. The tragedy—the disgrace, soto speak—is that the American scientific and educational establishment is not benefitting from the Chudnovskys’ assistance. Thirteen years have gone by since the Chudnovskys arrived here, and where are all the graduate students who would have worked with the brothers? How many truly great mathematicians have you ever heard of who couldn’t get a job? I think the Chudnovskys are the only example in history. This vast educational system of ours has poured the Chudnovskys out on the sand, to waste. Yet Gregory is one of the remarkable personalities of our time. When I go up to that apartment and sit by his bed, I think, My God, when I was a student at Harvard I was in contact with people far less interesting than this. What happens to me in Gregory’s room is like that line in the Gerard Manley Hopkins poem: ‘Margaret, are you grieving / Over Goldengrove unleaving?’ I’m grieving, and I guess it’s me I’m grieving for.”

"Two billion digits of pi? Where do they keep them?” Samuel Eilenberg said to me. Eilenberg is a gifted and distinguished topologist, and an emeritus professor of mathematics at Columbia University. He was the chairman of the department when the question of hiring the brothers first became troublesome to Columbia. “There is an element of fatigue in the Chudnovsky Problem,” he said. “In the academic world, we have to be careful who our colleagues are. David is a pain in the neck. He interrupts people, and he is not interested in anything except what concerns him and his brother. He is a nudnick! Gregory is certainly unusual, but he is not great. You can spend all your life computing digits. What for? You know in advance that you can’t see any regularity in pi. It’s about as interesting as going to the beach and counting sand. I wouldn’t be caught dead doing that kind of work! Most mathematicians probably feel this way. An important ingredient in mathematics is taste. Mathematics is mostly about giving pleasure. The ultimate criterion of mathematics is aesthetic, and to calculate the two-billionth digit of pi is to me abhorrent.”

“Abhorrent—yes, most mathematicians would probably agree with that,” said Dale Brownawell, a respected number theorist at Penn State. “Tastes change, though. If something were to begin to show up in the digits of pi, it would boggle everyone’s mind.” Brownawell met the Chudnovskys at the Vienna airport when they escaped from the Soviet Union. “They didn’t bring much with them, just a pile of bags and boxes. David would walk through a wall to do what is right for and his brother. In the situation they are in, how else can they survive? To see the Chudnovskys carrying on science at such a high level with such meagre support is awe-inspiring.

Richard Askey, a prominent mathematician at the University of Wisconsin at Madison, occasionally flies to New York to sit at the foot of Gregory Chudnovsky’s bed and learn about mathematics. “David Chudnovsky is very good mathematician,” Askey said to me. “Gregory is one of the few great mathematicians of our time. Gregory is so much better than I am that it is impossible for me to say how good he really is. Is he the best in the world or one of the three best? I feel uncomfortable evaluating people at that level. The brothers’ pi stuff is just a small part of their work. They are really trying to find out what the word ‘random’ means. I’ve heard some people say that the brothers are wasting their time with that machine, but Gregory Chudnovsky is a very intelligent man, who has his head screwed on straight and I wouldn’t begin to question his priorities. The tragedy is that Gregory has had hardly any students. If he dies without having passed on not only his knowledge but his whole way of thinking, then it will be a great tragedy. Rather than blame Columbia University, I would prefer to say that the blame lies with all American mathematicians. Gregory Chudnovsky is a national problem.”

"It looks like kvetching,” Gregory said from his bed. “It looks cheap and it is cheap. We are here in the United States by our own choice. I don’t think we were somehow wronged. I really can’t teach. So what does one want to do about it? Attempts to change the system are very expensive and time-consuming and largely a waste of time. We barely have time to do the things we want to do.”

“To reform the system?” David said playing his flashlight across the ceiling. “In this country? Look. Come on It’s much easier to reform a totalitarian system.”

“Yes, you just make a decree, Gregory said. “Anyway, this sort of talk moves into philosophical questions. What is life, and where does the money come from?” He shrugged.

Toward the end of the summer of 1991, the brothers halted their probe into pi. They had surveyed pi to two billion two hundred and sixty million three hundred and twenty-one thousand three hundred and thirty-six digits. It was a world record, doubling the record that the Chudnovskys had set in 1989. If the digits were printed in ordinary type, they would stretch from New York to Southern California. The brothers had temporarily ditched their chief competitor, Yasumasa Kanada—a pleasing development when the brothers considered that Kanada had access to a half-megawatt Hitachi monster that was supposed to be faster than a Cray. Kanada reacted gracefully to the Chudnovskys’ achievement, and he told Science News that he might be able to get at least a billion and a half digits of pi if he could obtain enough time on a Japanese supercomputer.

“You see the advantage to being truly poor. We had to build our machine, but now we get to use it, too,” Gregory said.

The Chudnovskys’ machine had spent its time both calculating pi and checking the result. The job had taken about two hundred and fifty hours on m zero. The machine had spent most of its time checking the answer, to make sure each digit was correct, rather than doing the fundamental computation of pi.

“We have done our tests for patterns, and there is nothing,” Gregory said. “It would be rather stupid if there were something in a few billion digits. There are the usual things. The digit three is repeated nine times in a row, and we didn’t see that before. Unfortunately, we still don’t have enough computer power to see anything in pi.”

Such was their scientific conclusion, and yet the brothers felt that they may have noticed something in pi. It hovered out of reach, but it seemed a little closer now. It was a slight sign of order—a possible sign—and it had to do with the running average of the digits. You can take an average of any string of digits in pi. It is like getting a batting average, an average height, an average weight. The average of the digits in pi should be 4.5. That’s the average of the decimal digits zero through nine. The brothers noticed that the average seems to be slightly skewed. It stays a little high through most of the first billion digits, and then it stays a little low through the next billion digits. The running average of pi looks like a tide that rises and retreats through two billion digits, as if a distant moon were passing over a sea of digits, pulling them up and down. It may or may not be a hint of a rule in pi. “It’s unfortunately not statistically significant yet,” Gregory said. “It’s close to the edge of significance.” The brothers may have glimpsed only their desire for order. The tide that seems to flow through pi may be nothing but aimless gabble, but what if it is a wave rippling through pi? What if the wave begins to show a weird and complicated pulsation as you go deeper in pi? You could become obsessive thinking about things like this. You might have to build more machines. “We need a trillion digits,” David said. A trillion digits printed in ordinary type would stretch from here to the moon and back, twice. The brothers thought that if they didn’t get bored with pi and move on to other problems they would easily collect a trillion digits in a few years, with the help of increasingly powerful supercomputing equipment. They would orbit the moon in digits, and head for Alpha Centauri, and if they lived and their machines held, perhaps someday they would begin to see the true nature of pi.

Gregory is lying in bed in the junk yard, a keyboard on his lap. He offers to show me a few digits of pi, and taps at the keys.

On the screen beside his bed, m zero responds: “Please, give the beginning of the decimal digit to look.”

Gregory types a command, and suddenly the whole screen fills with the raw Ludolphian number, moving like Niagara Falls. We observe pi in silence for quite a while, until it ends with:

. . . 18820 54573 01261 27678 17413 87779 66981 15311 24707 34258 41235 99801 92693 5256192393 53870 24377 10069 16106 22971 02523 30027 49528 06378 64067 12852 77857 42344 28836 88521 72435 85924 57786 36741 32845 66266 96498 68308 59920 06168 63376 85976 35341 52906 04621 44710 52106 99079 33563 54625 71001 37490 77872 43403 57690 01699 82447 20059 93533 82919 46~19 87044 02125 12329 11964 10087 41341 42633 88249 48948 31198 27787 03802 08989 05316 75375 43242 20100 43326 74069 33751 86349 40467 52687 79749 68922 29914 46047 47109 31678 05219 48702 00877 32383 87446 91871 49136 90837 88525 51575 35790 83982 20710 59298 41193 81740 92975 31.

“It showed the last digits we’ve found,” Gregory says. “The last shall be first.”

“Thanks for asking,” m zero remarks, on the screen.