Space-Time
and a Finite Model

Notes by Steven H. Cullinane
May 28, 2007

Part I: A Model of Space-Time

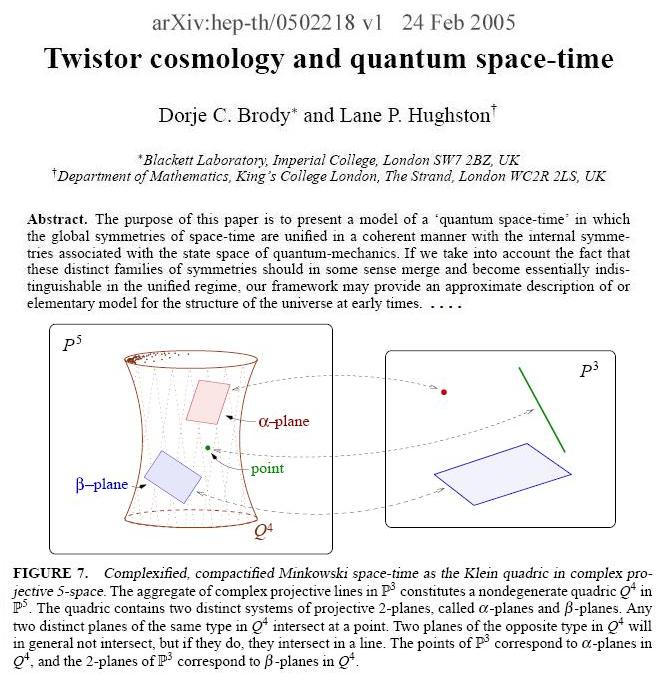
The following paper includes a figure illustrating Penrose's model of "complexified, compactified Minkowski space-time as the Klein quadric in complex projective 5-space."

For some background on the Klein quadric and space-time, see Roger Penrose, "On the Origins of Twistor Theory," from Gravitation and Geometry: A Volume in Honor of Ivor Robinson, Bibliopolis, 1987.

Part II: A Corresponding Finite Model

The Klein quadric also occurs in a finite model of projective 5-space.  See a 1910 paper:

G. M. Conwell, The 3-space PG(3,2) and its group, Ann. of Math. 11, 60-76.

Conwell discusses the quadric, and the related Klein correspondence, in detail.  This is noted in a more recent paper by Philippe Cara:

As Cara goes on to explain, the Klein correspondence underlies Conwell's discussion of eight heptads.  These play an important role in another correspondence, illustrated in the Miracle Octad Generator of R. T. Curtis, that may be used to picture actions of the large Mathieu group M₂₄.

Related material:

The projective space PG(5,2), home of the Klein quadric in the finite model, may be viewed as the set of 64 points of the affine space AG(6,2), minus the origin.

The 64 points of this affine space may in turn be viewed as the 64 hexagrams of the Classic of Transformation, China's I Ching.

There is a natural correspondence between the 64 hexagrams and the 64 subcubes of a 4x4x4 cube.  This correspondence leads to a natural way to generate the affine group AGL(6,2).  This may in turn be viewed as a group of over a trillion natural transformations of the 64 hexagrams.

See

Finite Geometry of
the Square and Cube



and

Geometry of the I Ching.

"Once Knecht confessed to his teacher that he wished to learn enough to be able to incorporate the system of the I Ching into the Glass Bead Game.  Elder Brother laughed.  'Go ahead and try,' he exclaimed.  'You'll see how it turns out.  Anyone can create a pretty little bamboo garden in the world.  But I doubt that the gardener would succeed in incorporating the world in his bamboo grove.'"

-- Hermann Hesse, The Glass Bead Game,
    translated by Richard and Clara Winston

---

Transcript of relevant text for search engines:

Part I--

From "Twistor cosmology and quantum space-time," by Dorje C. Brody (Imperial College, London) and Lane P. Hughston (King's College London):

FIGURE 7. Complexified, compactified Minkowski space-time as the Klein quadric in complex projective 5-space. The aggregate of complex projective lines in P³ constitutes a nondegenerate quadric Q⁴ in P⁵. The quadric contains two distinct systems of projective 2-planes, called alpha-planes and beta-planes. Any two distinct planes of the same type in Q⁴ intersect at a point. Two planes of the opposite type in Q⁴ will in general not intersect, but if they do, they intersect in a line. The points of P³ correspond to alpha-planes in Q⁴, and the 2-planes of P³ correspond to beta-planes in Q⁴.

Published in XIX Max Born Symposium, Wroclaw (Poland), 28 September - 1 October 2004, Springer, 2004, pp. 57-95

Part II--

From "RWPRI Geometries for the alternating group A₈," by Philippe Cara, Department of Mathematics, Vrije Universiteit Brussel

It is well known that the lines of PG(3,2) correspond to the 35 points of a hyperbolic quadric Q⁺(5,2) with equation X₀ X₁ + X₂ X₃ + X₄ X₅ = 0 in the five-dimensional projective space PG(5,2). This correspondence is known as the Klein correspondence and the hyperbolic quadric is then called the Klein quadric. In what follows, the Klein quadric will be denoted by Q. On Q there are two families of 15 planes each, which correspond to the 15 points and the 15 planes of PG(3,2) respectively. Two different planes of the same family have one point in common and two planes of different families are either disjoint or share one line. A {point, plane}-flag p*P of PG(3,2) appears on Q as two planes from different families which intersect in a line, representing the three lines in PG(3,2) which are included in P and contain the point p. The Klein correspondence for PG(3,2) is described in detail in [14].

_{[14] G. M. Conwell, The 3-space PG(3,2) and its group, Ann. of Math. 11 (1910), pp. 60-76}

_{Published in Finite Geometries: Proceedings of the Fourth Isle of Thorns Conference (July 2000), Springer, 2001, ed. Aart Blokhuis, James W. P. Hirschfeld, Dieter Jungnickel, and Joseph A. Thas, pp. 61-97}