|
A nice discussion of map coloring can
be found in "The Mathematics of
Map Coloring," which Professor H.S.M. Coxeter wrote for the Journal of
Recreational Mathematics, 2:1 (1969). He began by pointing out that in
almost any atlas, 5 or 6 colors are used in a map of the United States
to distinguish neighboring states.
|
|
| |
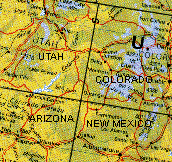
"Apparently the artist did not
realize that four
colors would have sufficed. (It is understood that two states may be
colored
alike if they merely have a point in common, as in the case of Arizona
and Colorado.)" This leads to the mathematical question,
Can every conceivable map (on a sphere or a plane) be
colored with four colors, or does some particular map really need five?
|
|
|
| |
The question was first
posed in
1852 by Francis Guthrie, a mathematics graduate student in London at
the time. He had noticed the sufficiency of four colors for
distinguishing the counties in a map of England. The question was
passed along to several important British mathematicians (De Morgan,
Hamilton), but apparently it was not seriously investigated until
Cayley in 1878 challenged the members of the London Mathematical
Society to solve it. From that time until its computer solution nearly
100 years later the problem stood alongside Fermat's last theorem among
the great mathematical challenge of the century. Like the Fermat
problem, the map-coloring question is easily stated and can easily be
understood by anybody. Both problems lack any important consequences,
yet have led to extraordinarily important new mathematical ideas and
techniques. Both problems are alluring and elusive.
|
|
| |
It is very easy to show
that six colors
suffice, and five is not much harder -- indeed, the proof that five
colors suffice can be found in many elementary textbooks and expository
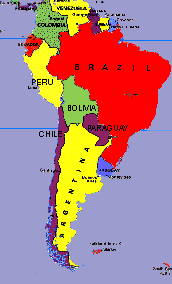
articles. It is also easily seen that three colors are not enough -- in
fact, four are needed to color Bolivia and its five neighboring States
(Brazil, Peru, Chile, Argentina and Paraguay). As Francis Guthrie long
ago observed, every map with only a small number of countries can
easily be colored with only four colors; the challenge is to prove that
four colors suffice for every conceivable map.
The proof that every planar map is four colorable was
achieved in 1976 by Kenneth Appel and Wolfgang Haken, working together
at the University of Illinois at Urbana-Champaign with the substantial
help of a computer. An expanded version of their proof, including
numerous corrections and philosophical comments, is found in their
later monograph Every Planar Map is Four Colorable, Contemp. Math.,
vol. 98, Amer. Math. Soc., Providence, RI, 1989. Their accomplishment
was announced at the University of Toronto during the 1976 summer
meeting of the American Mathematical Society. The announcement set off
a debate concerning the nature of mathematical proofs.
|
 |
| |
Even though no human has every gone
through Appel and Haken's entire proof, there is no doubt today that
the result is correct. It has been independently checked using
different techniques and different computers. For the latest word see
Robin Thomas, An Update on the Four-Color Theorem, Notices of the Amer.
Math. Soc. 45:7 (August 1998) 848-859 (an authoritative expository
article that contains the historical and philosophical background
together with an outline of the relevant mathematics and a discussion
of the various proofs). On the other hand, to many mathematicians a
proof must explain why the result must be true; all current proofs of
the four-color theorem are a long way from that criterion.
There is an elementary text (in English) devoted to the
theorem.
David Barnette, Map Coloring, Polyhedra, and the Four-Color
Problem.
The Dolciani Mathematical Expositions, 8. Mathematical Association of
America, Washington, D.C. 1983.
For those who read German, there is a somewhat
more
sophisticated, delightfully written account giving both the historical
and mathematical background for the non-specialist.
Rudolf Fritsch, Der Vierfarbensatz: Geschicte, topologische
Grundlagen und Beweisidee. Bibliographisches Institut, Mannheim, 1994.
|
|

