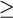Cached from the Newsletter of the New Zealand Mathematical Society, December 2003, http://www.massey.ac.nz/~wwifs/mathnews/NZMS89/news89a.shtml

TWELVE SPORADIC GROUPS
by Robert L. Griess, Jr. Springer Monographs in Mathematics, Springer-Verlag, Berlin, 1998, 169 pp, US$79.95. ISBN 3-540-62778-2

One of the crowning achievements of mathematics in the 20th century has to be the classification of the finite simple groups. Completed in 1980, this involved research by dozens of mathematicians over the course of decades, and published in some 10,000 pages of journal articles. One of the final steps (in 1980) was a proof by Robert Griess of the existence of the Monster, a group of order 2⁴⁶· 3²⁰· 5⁹· 7⁶· 11²· 13²· 17· 19· 23· 29· 31· 41· 47· 59· 71.  Every finite group G can be decomposed as a subnormal series  of subgroups {G_i} with simple factors G_i/G_i-1, such that no further refinement is possible, and in this way the finite simple groups are the "building blocks'' for all finite groups — somewhat analogous to the elements in chemistry. The classification says that every finite simple group lies in one of four main classes: cyclic groups C_p of prime order p, alternating groups of degree A_n of degree n 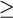5, various simple groups of Lie type (certain families of matrix groups over finite fields, including the classical groups as well as exceptional families), and 26 "sporadic'' groups that do not fall into of the first three classes.

The largest of the sporadic simple groups is the Monster, and 20 of the 26 sporadics are involved in the Monster as subgroups or as quotients of subgroups. These 20 (called the "Happy Family'') themselves occur naturally in three generations, and this book concerns the 12 groups in the first two of these generations, all related to the Golay codes and the Leech lattice (namely the five Mathieu groups, the three Conway groups, and the groups of Hall-Janko, Higman-Sims, Suzuki and McLaughlin). The book aims to promote the understanding of these groups, and complements two other books on the sporadics: "Sporadic groups'' by Michael Aschbacher (Cambridge Univ. Press, 1994), and "Geometry of sporadic groups'' by Sasha Ivanov (Cambridge Univ. Press, 1999). The two latter texts are important but rather technical, while the book under review is written in a way to help the reader "appreciate their beauty, linger on details and develop unifying details in their structure theory''. It is certainly accessible to graduate students having a good basic knowledge of linear and abstract algebra, permutation groups and matrix groups.

The first two chapters provide some necessary background from the theory of groups, modules, finite geometry, group cohomology (including extensions and Schur multipliers), bilinear forms, group presentations, and root systems. Most of this is given without proofs (but with some helpful references). Chapters 3 to 7 deal with linear error-correcting codes and their automorphism groups, the Hexacode (a linear code of length 6, dimension 3, and minimum weight 4 over the field GF(4)), the binary Golay code (a [24,12,8]-code over GF(2)), the Mathieu group M₂₄ and its subgroups, the ternary Golay code (constructed from a [4,2,3] ternary code), and its automorphism group 2· M₁₂ (the covering group of the Mathieu group M₁₂). Detailed analysis is given, including existence and uniqueness proofs, but some aspects are (deliberately) incomplete. Chapters 8 to 10 deal with lattices, the Leech lattice 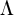(a lattice in 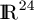with extremely nice properties) and its automorphism group, the Conway groups (each of which is a subgroup of quotient of a subgroup of Aut(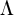)), and the other four sporadic simple groups involved in Aut(). 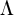Details of many proofs are suppressed, but additional information is given in appendices to Chapter 10. Finally Chapter 11 offers a brief account of the eight remaining groups in the Happy Family (all of which are involved in the Monster), plus the six "pariahs'' (the remaining six of the 26 sporadic groups, namely three of the four Janko groups, plus the Lyons, O'Nan and Rudvalis groups).

This book is interesting and informative, and achieves its aims well. The exposition is spoiled a little by numerous misprints and errors (some transposed from their source, but many new, giving the impression of insufficient proof-reading), and a few unfortunate personal comments about historical attribution. These aside, the book contains some beautiful and significant mathematics, presented in a user-friendly style, and is well worth reading

Marston Conder
The University of Auckland