Talk:Four color theorem/archive2
From Wikipedia, the free encyclopedia.
Dharwadker's proof
What about this proof? [1] Julyo 16:23, 13 July 2005 (UTC)
- Be very careful. The web page mentioned by Julyo first
appeared a few years ago, maybe around 2001. As far as I can tell, this
work has never appeared in a peer-reviewed journal. I base this claim
on a search for "Dharwadker" on MathSciNet: only one paper turns up,
and does not appear to have anything to do with the four colour theorem.
This proof first appeared in 2000. The Canadian Mathematical Society
website "Knot a Braid of Links" review shows the date October 5, 2000 [2]
- Dharwadker's "proof" is described and acclaimed on many popular
mathematical websites, as a quick Google search shows. One site even
states that his proof has "stood the test of time". I am very skeptical
that his proof is correct, or that it even makes sense at all. I don't
know enough about Steiner systems or Eilenberg modules (technical
devices mentioned on that page) to be able to check the proof. I
suspect that most people are similarly ignorant.
Well depends on who you mean by "most people". The average
mathematician should be sufficiently conversant with group theory,
topology and combinatorics to be able to read through the proof.
- Of course, if you read the proof yourself and understand it, then
by all means, you are free to believe it. But the scientific community
does not appear to have accepted it at this time. Dmharvey
 Talk 19:32, 13 July 2005 (UTC)
Talk 19:32, 13 July 2005 (UTC)
Ironically, Kempe's "proof" was "accepted" by the mathematical
community by your definition. Kempe's "proof" was published in a top
american math journal, peer reviewed and all that. Kempe was even
knighted by the queen of England! But Kempe's proof was wrong.
Dharwadker's proof seems to be very clearly written and surely, if
there were any errors in the proof, someone would have pointed them out
by now? Dharwadker's website seems to be very well-known.
-
- Thank you; I was wondering about that for a long time...and though
I still can't understand it, I started to think that it was bullshit
after not noticing it in either MathWorld or Wikipedia even though the
"proof" has been on the Internet (on a craptacular Geocities account,
no less!) since 2000 (at least that's when I first found Dharwadker's
page). I noticed that at the end, it sounds as if it is saying
something about graph-coloring on the sphere, which is NOT the same as
the plane case dealt with in the four-color theorem. Julyo 06:19, 14 July 2005 (UTC)
-
-
- Actually, graph-colouring on the sphere is the same as on
the plane, at least for maps with finitely many regions. The easiest
way to see this is: take your map on the sphere, pick one region and
call it the "infinite" region, cut a little hole out of the middle of
the infinite region, and then "open the hole out" while flattening out
the remaining regions onto the plane. Dmharvey
 Talk 11:06, 14 July 2005 (UTC)
Talk 11:06, 14 July 2005 (UTC)
Yes, Julyo needs a first course in topology!
-
- I am guessing that the reason nobody has pointed out any errors in
Dharwadker's proof is that he has not submitted it to the appropriate
forum. (Or perhaps he has, and got rejected.)
- You are of course, free to believe anything you read on the internet. Dmharvey
 Talk 17:02, 3 August 2005 (UTC)
Talk 17:02, 3 August 2005 (UTC)
-
-
- Surely, it would be published if there were no errors in it. Note also that the recent paper [3]
does not seem to mention mention Dharwadker, so it is not that well
known. I am also very skeptical about Dharwadker's paper: its
presentation feels rather nonstandard, it mentions things like Steiner
systems that are not generally known by mathematicians, though rather
elementary, but it has very little graph theory, some of the proofs are
quite high level and some of them are extremely detailed. I didn't find
any mistakes, but I don't think it's worth my time to go through it. --
Jitse Niesen (talk) 17:53, 3 August 2005 (UTC) (via edit conflict)
Steiner systems are well-known and I did not find anything any thing
"nonstandard" in the proof. The four color theorem can be stated purely
topologically, without any reference to graph theory. In fact a
substantial part of graph theory developed in trying to prove the four
color theorem. So, it is by no means necessary that a proof of the four
color theorem should even mention graphs!
-
-
-
- Although I agree that the proof is almost certainly fallacious, I
disagree that any accurate nontrivial results should be published in a
well-known formal forum. There are many results that originated from
informal notes and letters of famous people. Often these are only
collected into some formal publishing at a later time. However,
Dharwadker is not a famous person, and even if he is correct, generally
nobody cares about a simpler proof of a known result unless they're
writing a textbook or it helps to generate other new results. This is
the same reason people say that sci.math troll James Harris is wasting
his time with his fallacious proof of Fermat's Last Theorem. Deco 18:38, 3 August 2005 (UTC)
Why do you think the proof is fallacious? I did not find anything wrong in it.
- OK. I took a deep breath and actually tried to read some of the
paper. My conclusion is that it's absolute rubbish. If Dharwadker
becomes famous for this one day, I'll eat my words. Here's his overall
plan. He says: take a particular map m, and a particular
colouring of that map with N colours, when N is the minimal number of
colours necessary to colour every planar map. So far so good. Then he
uses this m to construct a Steiner system
with certain properties. Then he uses Tits' inequality to show that
such a Steiner system can only exist if N ≤ 4. Hmmmm. Rather
suspiciously, his construction of the Steiner system does not depend on any properties of m. It doesn't matter if m can be coloured in fewer colours — it doesn't even matter if m contains adjacent countries of the same colour.
Well, actually the proof does depend crucially on the properties of M(N). Using the notation in the proof -
1) The map M(N) cannot be colored with less than N colors because
then some of the elements of the group algebra will represent empty
sets of regions and the group actions cannot be defined.
2) The map M(N) cannot be colored with more than N colors because
then some of the elements of the group algebra will represent unions of
multiple regions (modulo N), violating the topological subdivision of
the riemann surface.
-
- I'm afraid I still disagree. I think there is some confusion between "The map M(N) cannot be coloured with less than N colours" and "The map M(N) is not
coloured with less than N colours". (Remember that the whole setup in
Dharwadker's proof is that M(N) is a particular map with a particular colouring, fixed throughout the proof).
- To make the distinction clearer, think about your point (2). Clearly this has to mean "The map M(N) is not coloured with less than N colours", because the other interpretation — "M(N) cannot
be coloured with more than N colours — would be ridiculous. Of course I
can colour it with more than N colours. For example if it has 20
regions, I can colour it using 20 different colours.
- Similarly, in point (1), you must mean "The map M(N) is not
coloured with less than N colours". And under this interpretation,
you're completely right about the group algebra breaking down. And
Dharwadker does use the fact that M(N) is not coloured with less than N colours, but he never uses the fact that M(N) cannot be coloured with fewer than N colours. He says that he uses this, over and over again (a few too many times perhaps), but he doesn't actually use it anywhere. Please could you point out the place where he actually
uses it. (And while you're at it, please point out where he actually
uses the fact that m(N) doesn't have adjacent countries with the same
colour.) Dmharvey
 Talk 11:35, 4 August 2005 (UTC)
Talk 11:35, 4 August 2005 (UTC)
No, no. Points (1) and (2) show that the the proof does depend
crucially on the properties of M(N). They show exactly how the proof
would break down if the properties of M(N) were violated. This kind of
argument is needed to show that hypotheses are actually used in a
proof. For example, in Wiles's proof of Fermat's Last Theorem, where is
the hypothesis n>2 actually used? It must be shown that it is used
because otherwise Wiles's proof would prove Pythagoras's theorem is
false! In order to see this one must put n=2 in Wiles's proof and find
out exactly where it breaks down (assuming it is correct).
- In other words, he has proved: Dharwadker's theorem: Given any
planar map, and a particular colouring of that map — where you can use
as many colours as you like, and neighbouring countries may be assigned
the same colour if you so please — then you've really only used four colours!
No, read the statement of the theorem and read the proof!
- Again: if I hand a map with five regions using five distinct
colours to Dharwadker, he should be able to use his proof to construct
for me a certain Steiner system which Tits' inequality guarantees
cannot exist.
Why? Your map would violate the definition of M(N).
- (In fact I don't even think his construction uses the planarity of the map in any essential way, which only adds to the entertainment value.)
Why not? Are you familiar with riemann surfaces?
-
- Yes I am familiar with riemann surfaces. The reason I added this as
a parenthetical comment afterwards is that I'm not so sure about it as
I was about the previous things. I agree that his construction uses the
planarity to the extent that it is necessary to the embedding that he
carries out, but for the reasons I outlined above, I don't think this
matters. Dmharvey
 Talk 11:35, 4 August 2005 (UTC)
Talk 11:35, 4 August 2005 (UTC)
Yes, it matters crucially. The group actions use the winding number around the branch point.
- In addition, it's worth pointing out that any paper purporting to
prove the four colour theorem shouldn't be wasting its time giving
proofs of Tits' inequality let alone Hall's marriage theorem concerning perfect matchings. These are not exactly new results.
You are familiar with Jaques Tits' work? Good for you!
-
- No I'm not familiar with Tits' work. However, the inequality that Dharwadker uses in his proof appears to be well known. Dmharvey
 Talk 11:35, 4 August 2005 (UTC)
Talk 11:35, 4 August 2005 (UTC)
- Ah well, at least I got to learn something about Steiner systems along the way.
Dmharvey  Talk 19:23, 3 August 2005 (UTC)
Talk 19:23, 3 August 2005 (UTC)
- And just for the record: although Kempe's proof was wrong, the
reason we remember him so well is that his briliant ideas lie at the
absolute heart of the modern successful computer-based proofs. Dmharvey
 Talk 19:27, 3 August 2005 (UTC)
Talk 19:27, 3 August 2005 (UTC)
I think we should mention Dharwadker's proof in the main article (or at least provide a link to it).
Recent anonymous poster is probably Dharwadker himself
No, my name is Bob!
- If I'm right, then at the very least, he is behaving in a very un-wiki manner.
Does the wiki manner discourage discussion?
- I don't have enough evidence to convict, but it's mighty suspicious. Let's see what we've got so far.
- (By the way, I'm taking a big risk doing this, because it looks
like Dharwadker has already tried to ruin some reputations along the
way. I'll get to that in a moment. I'm sure he'll try to delete this
post, and probably impersonate me as well.)
Hope Dharwadker doesn't see this! It is very mean of you to make
such unfounded allegations. It might be construed that you have some
vested interests.
- The anoymous poster at one point argued that
- 1) The map M(N) cannot be colored with less than N colors
because then some of the elements of the group algebra will represent
empty sets of regions and the group actions cannot be defined.
- 2) The map M(N) cannot be colored with more than N colors
because then some of the elements of the group algebra will represent
unions of multiple regions (modulo N), violating the topological
subdivision of the riemann surface.
- The above text was copied verbatim from http://fourcolourtheorem.tripod.com/.
This page claims to be a review of Dharwadker's proof, by someone
called Robert Stewart. (By the time you read my post, this site will
probably be removed or edited. Try Google's cached copy.)
No, the site is still there. Would you like a pdf copy of my review?
- Interestingly, the review is dated 31 July 2005, which is four days
ago. Keep in mind that Julyo and I started having this discussion here
about two weeks ago.
No, I didn't see your discussion until yesterday. I just thought that it may be a good idea to answer some of your questions.
- Now it starts getting a little complicated.
- There's a fellow by the name of Steven Cullinane who, some time
ago, put up a critique of Dharwadker's proof, saying essentially the
same things that I said above. Cullinane started getting abused heavily
by one Bob Stewart on various mailing lists. It took the form of an attack on Culinane's reputation. Cullinane describes the whole affair at http://www.log24.com/log05/050725-Crank.html. (Cullinane also has a very recent post (yesterday) describing the new tripod site.)
Yes, I did contribute to a discussion on sci.math with the title
"Steven Cullinane is a Crank". It is because of a link on Cullinane's
crank website that I saw Dharwadker's proof. I really like Dharwadker's
proof and I wrote a review that hopefully presents the proof in a more
accessible manner to people who are less familiar with some of the
heavy-duty algebra and topology used in the proof.
- (To be fair, I should also mention that Cullinane has in the past
criticised some mathematicians that I know quite personally, and whom I
think very highly of. I think his criticisms in those cases were a
little vitriolic and not justified. But in the case of Dharwadker, I
agree with him fully.)
What exactly do you agree with?
- Now it gets really interesting.
- The IP addresses used by the recent anonymous poster (203.101.*.*)
are all in a range owned by an ISP in India (Mantra Online). This
doesn't say much; India's a very big country, and that ISP appears to
run in many major Indian cities.
What would you like to know about me? You can email me at bobstewart_III@hotmail.com.
- Nevertheless, the only other contribution from such an IP address to Four color theorem occurred on 23/Sep/2004, which — surprise — involved an attempt to link to the geocities site containing Dharwadker's proof.
Why would you not want to link to the site? Do you have any vested interests?
- Even better: on the following day (24/Sep/2004), a similar IP address added a link to Roman surface,
to an article on "Roman Surfaces" on the same website. That link is
still there. I don't know anything about Roman Surfaces, so I have no
opinion on whether the material on that topic at Dharwadker's site is
quality or not. I suspect it's probably better than the stuff on the
four colour theorem.
I still do not understand your opinion on Dharwadker's proof (the mathematics part of it).
- In fact, a search for "Dharwadker" on Wikipedia only turns up three pages: Four color theorem, Roman surface, and a user page User_talk:Andris.
Andris is the editor who deleted the link to Dharwadker's page in 2004.
The message on Andris' talk page is signed by one Clarence Williams,
who posted to Andris's page with, again, the same IP address range. The
name Clarence Williams is also used on http://www.angelfire.com/mi4/proof/,
which is another link in the mini-web of Dharwadker-worship sites. As
Cullinane points out, it's impossible to find out anything more about
these people "Robert Stewart" and "Clarence Williams". And all of these
sites are hosted by free-hosting companies like geocities and
angelfire, which all reek of intended anonymity.
Oh, so this Andris had an opinion too? Mathematical or social?
My recommendation is not to take posts from this IP address range too seriously.
Dmharvey  Talk 14:48, 4 August 2005 (UTC)
Talk 14:48, 4 August 2005 (UTC)
Why not? Because a lot of heavy mathematics comes from this IP range?
- And of course I'm not going to bother any more trying to
demonstrate why his proof is flawed. I've wasted enough time on it
already. Everybody is free to make up their own minds. If Four color theorem
ends up with a link to Dharwadker's page, or any sympathetic
description of the proof, so much the worse for Wikipedia's reputation.
Dmharvey
 Talk 15:09, 4 August 2005 (UTC)
Talk 15:09, 4 August 2005 (UTC)
You haven't demonstrated anything! All you've demonstrated is that
you have already made up your mind about something and no amount of
mathematics is going to change that (or worse that you have a vested
interest). I hope that you may learn to keep a more open mind about
people and things.
hey there bob
- Hey there Ashay, or Bob, or Clarence, or Dharwadker, or
203.101.*.*, or whatever your real name is. (This is starting to sound
like Alice and Bob!) You're obviously pretty new to wikipedia, so let me try to explain a bit how it works.
My real name is Robert Stewart!
- It's a free-for-all. It's democracy at its absolute worst. So the
deal is: if you can convince the community that your link deserves to
be there, then good for you, you can have your link. I'll try to stop
you for a while, but if the community shouts me down, I'll respect that.
Why do you presume? All I'm trying to do is answer some of your questions!
- However, it's going to be more difficult than just putting up a few
pages on geocities or angelfire, or convincing Dr Matrix (or even the
Canadian Mathematical Society— very impressive!). There are a fair
number of decent mathematicians — actual real people who earn a living
by doing and/or teaching mathematics — who hang around these pages, and
I'm confident enough about my analysis of Dharwadker's proof that these
people would come down on my side if it came to an edit war.
These people care quite a lot about the accuracy of articles on
Wikipedia, and you might discover that they are willing to put in more
time than those who reviewed Dharwadker's article for the Math Forum.
I do have a page on tripod, but no affliation with the others that you mention! What is your analysis of Dharwadker's proof?
- If you do get your link, then I guess that's a major win for
Dharwadker's marketing drive, since Wikipedia articles generally rate
pretty highly on Google. On the other hand, if it turns out that the
proof is wrong, and that over the course of a long debate the essential
details of its incorrectness are recorded here, then that's a bad thing
for Dharwadker, for much the same reason. It's very difficult to make
stuff on Wikipedia disappear. That's not a threat; it's just a fact of
life that you should take into account (on Dharwadker's behalf).
It's not my link! Dharwadker's proof is correct.
- I believe that I have already explained why I think the proof is
incorrect. (And Jitse is still waiting for an answer to his question.)
I no longer feel I have a responsibility towards you to explain
my position on the mathematical content (or lack thereof). I've
adequately discharged my responsiblity to the community, so now it's up
to others to decide.
The proof is correct. Jitse should look up for his answer.
- Incidentally, if you actually are Dharwadker, then a quck Google
search turns up some professional information about you. But if you're
Bob Stewart, then I think we are all entitled to a little bit more
information about you than just a hotmail address.
I'm Bob! What info would you like?
- Now, I fully expect you to pepper my post with brief one-liners —
that's cool, you're allowed to do that — but I would prefer, for the
sake of other people trying to follow this discussion, that you add
your reply below my entire post. Also, could you please indent
your posts more sensibly in the future. And sign them, with Bob or
something. Even better, sign up for an account. Check out what other people do around here, you'll get the idea.
I now have my very own wiki account! Yours truly, Bob.
- May I add that this is by far the most interesting exchange I've ever had in my time at Wikipedia.
The pleasure is all mine! Rstewart
- Cheers, Dmharvey
 Talk 20:36, 4 August 2005 (UTC)
Talk 20:36, 4 August 2005 (UTC)
Further analysis of Dharwadker's proof
- Exactly. So, now take any map with five regions, colour every
region with a different colour, and please show us where the
construction breaks down. -- Jitse Niesen (talk) 17:27, 4 August 2005 (UTC)
In your map some of the regions will get identified modulo N. You
will not be able to show that the group actions are faithful. You will
not be able to prove that the blocks are unique. The construction of
the Steiner system will break down.
- Why will they be identified? As I understand it, all regions with
the same colour are identified. So, if you have a map with five regions
all of a different colour, none of the regions will be identified. -- Jitse Niesen (talk) 11:48, 5 August 2005 (UTC)
If no two regions in your map are identified modulo N then you are claiming that N=5 and the four color theorem is false!
- I don't understand you comment. Indeed, I am claiming for the sake
of argument that N=5 and the four colour theorem is false. Dharwadker's
paper purports to prove the four colour theorem, so it should say
somewhere why my example won't work. I can't find where it does so, so
I don't trust the paper. Incidentally, it would be helpful if you sign
your comments, which you can do by typing ~~~~ (four tildes). -- Jitse Niesen (talk) 12:34, 5 August 2005 (UTC)
-
- Agree with Jitse. You can't start the proof by assuming that N = 4.
That's what you're trying to prove. You should, as Dharwadker says
himself, start with the assumption that 4 <= N <= 6. This
includes the possiblity that N = 5, and Jitse is asking what goes wrong
in the construction if it turns out that N = 5.
-
- Incidentally I find it very odd that the paper mentions the "six
colour theorem" but not the "five colour theorem". It is barely more
difficult to prove that five colours suffice than that six colours
suffice. You just need to chase around a few Kempe chains (there's another article waiting to be written...), as any elementary book on the four colour theorem will explain. Dmharvey
 Talk 13:03, 5 August 2005 (UTC)
Talk 13:03, 5 August 2005 (UTC)
No, you are confusing two different things. N is well-defined (read
the definition of N in Dharwadker's proof). If you claim that N=5 then
you are claiming that the four color theorem is false. If, on the other
hand, you color your map with 5 colors then you cannot prove that no
two regions are identified unless you do claim that N=5. In which case
you are again claiming that the four color theorem is false and that
your specific map is a counter-example to the four color theorem! Rstewart 13:13, 5 August 2005 (UTC)
- As I said, I claim that N=5 and that my map is a counterexample. How does Dhardadker prove that I am wrong? -- Jitse Niesen (talk) 13:45, 5 August 2005 (UTC)
Dharwadker will ask you to show him your map. Rstewart 14:22, 5 August 2005 (UTC)
- Bob, could you please show Dhawadker the following map and ask him what he thinks about it:

This is Jitse's map
- Dmharvey
 Talk 15:00, 5 August 2005 (UTC)
Talk 15:00, 5 August 2005 (UTC)
If this is Jitse's map then it is not a counter-example to the four
color theorem. It can be colored properly with 4 colors and Dharwadker
would have proved Jitse wrong. Obviously the question was rhetorical:
Jitse cannot produce the map he claims. Dharwadker's proof is very
carefully written, please read the definitions carefully before making
your statements. Rstewart 16:12, 5 August 2005 (UTC)
- Yes, the map that Dmharvey showed will do. Since you can't or won't
answer my question, I see no reason to change my judgement that the
proof is very likely to be wrong and should not be included. -- Jitse Niesen (talk) 17:52, 5 August 2005 (UTC)
No, this map won't do. Your claim (see above) is that N=5 (which is
the assumption that the four color theorem is false) and that your map
is a counter-example. Clearly this map can be properly colored with 4
colors so it cannot be a counter-example. So you cannot ensure that no
two regions will get identified during your construction. Your
construction will break down at this point. Do you have any other
questions that I am not aware of? What reason do you have to believe in
your judgement? It is obvious to any mathematician who reads this
argument that you have no credible argument against Dharwadker's proof.
Dharwadker's proof is correct. Rstewart 09:04, 6 August 2005 (UTC)
-
- OK Bob, what about this map?
This is Jitse's second map, let's hope we don't need to produce a third
-
- Dmharvey
 Talk 19:44, 5 August 2005 (UTC)
Talk 19:44, 5 August 2005 (UTC)
Well, this map has the same problem. You must prove that it is a
counter-example to the four color theorem (if you want to ensure that
no two regions will be identified during your construction). Otherwise
your construction will break down. Clearly this line of argument is not
getting you anywhere! It is obvious to any mathematician who reads this
argument that you have no credible argument against Dharwadker's proof.
Dharwadker's proof is correct. Rstewart 09:04, 6 August 2005 (UTC)
- So Bob, you're saying that "Jitse's second map" can be coloured with four colours? Dmharvey
 Talk 10:40, 6 August 2005 (UTC)
Talk 10:40, 6 August 2005 (UTC)
Jitse must prove his claim (however absurd) about his second map if
he wishes to carry out the construction of his Steiner system without
break down. His claim is (see above) that this map is a counter-example
to the four color theorem. If he cannot prove his claim, he will not be
able to show that in his map no two regions will get identified modulo
N. He will not be able to show that the group actions are faithful. He
will not be able to prove that the blocks are unique. The construction
of his Steiner system will break down. This was Jitse's original
question (see above): Jitse wanted to know how the construction breaks
down if some of the hypotheses in Dharwadker's proof were not used. I
have shown you exactly how. Dharwadker's proof is correct.
- Bob, it's a simple yes/no question. Don't try to answer it with an entire paragraph. Let me ask it again.
- Can "Jitse's second map" be coloured with four colours? Dmharvey
 Talk 11:48, 6 August 2005 (UTC)
Talk 11:48, 6 August 2005 (UTC)
According to Jitse's claim he seems to believe it cannot be colored
properly with less than 5 colors. We have to keep an open mind.
- Bob, I don't want to know Jitse's opinion, I want to know your opinion.
It is a simple yes or no question. I'm trying to keep this really basic
for the sake of our readers whose mathematical experience is not as
deep as yours. Please answer the question, to the best of your
knowledge, with either the single word "yes" or the single word "no":
- Can "Jitse's second map" be properly coloured with four colours? Dmharvey
 Talk 12:22, 6 August 2005 (UTC)
Talk 12:22, 6 August 2005 (UTC)
Good morning! I appreciate your friendly tone! In my opinion,
Dharwadker's proof is correct, so the four color theorem is true and so
any map on the plane can be properly colored with at most 4 colors. So
the answer to your question is Yes. Rstewart 12:38, 6 August 2005 (UTC)
- Good. Thank you.
- Now I have another, very simple, yes/no question for you.
- In Dharwadker's proof, is it permissible, or is it not permissible, to take m(N) to be "Jitse's second map", with the colouring that I have illustrated above? Dmharvey
 Talk 12:48, 6 August 2005 (UTC)
Talk 12:48, 6 August 2005 (UTC)
You have come around full circle in your logic! If you can prove
that Jitse's second map with the coloring you have illustrated does
satisfy the definition of Dharwadker's M(N), then yes. Else, not
necessarily. The definition of Dharwadker's M(N) is decidedly
nontrivial. It uses the full force of Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC). Rstewart 13:08, 6 August 2005 (UTC)
- I would like to know your opinion, not mine.
- Please answer the question.
- In Dharwadker's proof, is it permissible, or is it not permissible, to take m(N) to be "Jitse's second map", with the colouring that I have illustrated above? Dmharvey
 Talk 13:20, 6 August 2005 (UTC)
Talk 13:20, 6 August 2005 (UTC)
Does Jitse's second map satisfy Dharwadker's definition of M(N)? If
so, then YES it is permissible. If not, then NO it is not permissible.
It is not a matter of opinion. Perhaps the question is undecidable in
ZFC in which case nobody could possibly have an opinion. Maybe it is
decidable in ZFC in which case everyone could have a justifiable
opinion. Not all questions in mathematics have Yes/No answers. To
answer the question you would have to compare Jitse's second map and
its coloring with all maps and all their colorings. The universal
quantifier involved in the question certainly shows that the question
is nontrivial. At any rate, Dharwadker proves that there exists a map
that satisfies the definition of M(N) and that's the only map he needs
for his proof. Rstewart 14:07, 6 August 2005 (UTC)
- OK, you have said that the answer to my question depends on whether Jitse's second map satisfies Dharwadker's definition of m(N). So let's take a step back, and ask that question instead:
- In your opinion, does Jitse's second map, with the colouring shown above, satisfy Dharwadker's definition of m(N)? Dmharvey
 Talk 14:54, 6 August 2005 (UTC)
Talk 14:54, 6 August 2005 (UTC)
To form an opinion I would have to compare Jitse's second map with
the coloring that you have illustrated with all maps and all colorings
to check whether it satisfies Dharwadker's definition of M(N). Even if
it were possible to do that, why would I be interested in forming such
an opinion? Dharwadker proves that there exists a map that satisfies
the definition of M(N) and that's the only map he needs for his proof. Rstewart 15:38, 6 August 2005 (UTC)
- I agree that there exists a map satisfying the definition of m(N). What I am actually asking is whether Jitse's map, with the indicated colouring, satisfies the definition of m(N).
- Do I understand correctly that you do not know whether his map, with the given colouring, satisfies the definition of m(N)? Dmharvey
 Talk 16:28, 6 August 2005 (UTC)
Talk 16:28, 6 August 2005 (UTC)
There is an infinite class of maps like Jitse's map (each with many
possible colorings). For each such map, either the map (with a given
coloring) satisfies Dharwadker's definition of M(N) or it does not.
Dharwadker has shown the existence of a map that satisfies the
definition of M(N) and that is the only map he needs for his proof.
What is the relevance of Jitse's map to all this? Jitse's map also
exists and either satisfies the definition of M(N) or doesn't (why
should I care which, unless it is somehow of relevance to the proof?). Rstewart 16:47, 6 August 2005 (UTC)
- Bob, could you please answer the question that I asked. You seem to
be the only person around who knows enough about Dharwadker's proof to
do so. The relevance of my question is something that other people
reading this can decide for themselves.
- Here it is again:
- Is it true that you do not know whether Jitse's second map, with the given colouring, satisfies the definition of m(N)? Dmharvey
 Talk 17:03, 6 August 2005 (UTC)
Talk 17:03, 6 August 2005 (UTC)
No, your question is completely irrelevant! There is an infinite
class of such irrelevant decision problems! Dharwadker's proof makes no
use of Jitse's map. Jitse's map was drawn to answer Jitse's question
(see above). After that question was answered, Jitse's map has no
further relevance. It is becoming painfully obvious that you have no
further questions. Dharwadker's proof is correct. Rstewart 17:42, 6 August 2005 (UTC)
- Robert.
- Allow me to point out that in the current climate, any link to Dharwadker's proof that you place on the Four color theorem page would last less than ten minutes. That's a fact; it's not something you can spin
away. I am offering you the opportunity to explain certain details of
how the proof works, details that I cannot otherwise understand, by
answering my very simple, very clearly stated questions. I cannot
compel you to answer them; all I can do is ask them of you repeatedly,
with varying degrees of politeness. You are completely free to leave this discussion any time you choose, and you are free to attempt to place your link.
- Therefore, for the third time:
- Do you know, or do you not know, whether Jitse's second map, with the supplied colouring, satisfies the definition of m(N)? Dmharvey
 Talk 18:04, 6 August 2005 (UTC) (via edit conflict)
Talk 18:04, 6 August 2005 (UTC) (via edit conflict)
You have taken the trouble to draw Jitse's second map and color it
with 5 colors. I have not checked whether the coloring is proper, but
let me assume that it is proper. Now, check (you can do this in a
finite number of steps) if you can find a proper coloring of Jitse's
second map with 4 colors. If you can do that, then Jitse's second map
with the 5 coloring does not satisfy the definition of Dharwadker's
M(N). But don't expect me to find an explicit 4 coloring for you, I
have better things to do! And I know that Dharwadker's proof is
correct. Rstewart 09:52, 7 August 2005 (UTC)
And tell me Harvey, what was the relevance of your question to
Dharwadker's proof? Clearly any questions in this line of reasoning are
going to essentially bring you back to Jitse's original question, which
has already been answered. Dharwadker's proof is correct. Rstewart 10:02, 7 August 2005 (UTC)
- Bob, you have now used the phrase "Dharwadker's proof is correct"
eight ten eleven times. Perhaps you would like to help us at Wikipedia by writing an article on proof by repetition? (Just click the link and start typing!) - Regarding relevance of my questions: please be patient. I am
getting there one baby step at a time. Your style of conversation
leaves me with little choice.
- Back to business. You have now admitted two interesting things.
- You admitted (at 12:38 on August 6th) that Jitse's second map can be properly coloured with four colours.
- You admitted (at 10:02 on August 7th) that if Jitse's second map can be properly coloured with four colours, then Jitse's second map, with the supplied 5-colouring, does not satisfy Dharwadker's definition of m(N).
- Therefore, although the following question is exceedingly similar to the question I have already asked three times:
- Surely you agree (see syllogism) that Jitse's second map, with the given 5-colouring, does not satisfy Dharwadker's definition of m(N)? Dmharvey
 Talk 10:48, 7 August 2005 (UTC)
Talk 10:48, 7 August 2005 (UTC)
No, I don't have any time to waste on irrelevant piecemeal
questions! Ask a relevant question all at one time! Otherwise, go away.
Rstewart 14:20, 7 August 2005 (UTC)
Completed review of Dharwadker's proof
A PROCLAMATION
- WHEREAS Dharwadker has refused to answer a simple question concerning his "New Proof of the Four Color Theorem"; and
- WHEREAS the question has been asked four times in succession; and
- WHEREAS Dharwadker employed deceptive means (including assuming multiple personas) to defend his "proof";
- THEREFORE let it be recognised that Dharwadker's proof is declared invalid and shall not be linked to by Wikipedia.
- (This proclamation shall be rendered void following any decision by
Dharwadker (or any of his associates) to rejoin the discussion by
answering the simple question posed above.)
Dmharvey  Talk 15:16, 7 August 2005 (UTC)
Talk 15:16, 7 August 2005 (UTC)
I don't think Dharwadker even knows about the existence of this discussion! Why do you think he does? I am Rstewart who is answering your questions (the ones that are even remotely relevant to Dharwadker's proof)
Perhaps you question was not relevant to the said proof?
Yes, you are wasting wiki disk space by repeating your questions that nobody is interested in answering!
You are paranoid! Do you see Dharwadker everywhere? Maybe he's
watching you right now! What's that... a shadow.... must be Dharwadker!
Oh? Why is it invalid? I think Dharwadker's proof is correct and I'm
sure a lot of other people do too! In fact, you are the first person I
know who seem to passionately believe that it is not correct (without
any valid reasons though). I thought that wiki was a democracy. And why
do you think that I would want to add any links? Why should I care?
Well, I'm here to answer any relevant questions. I don't know about any others.
Maybe Dharwadker won't read your proclaimation! Rstewart 15:36, 7 August 2005 (UTC)
Lemma 8 of Dharwadker's paper
- The proof of Lemma 8 in Dharwadker's paper is incorrect. The statement of the lemma is:
- H = S3 is a subgroup of G = Sym(ZN]S3). There exists k = [G:H] elements ψ1,...,ψk of G such that {ψ1H,...,ψkH} is the family of left cosets and {Hψ1,...,Hψk} is the family of right cosets.
- The proof goes as follows. First, elements ψ1,...,ψk of G are chosen such that the left cosets Hψi and Hψj are distinct if
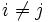 . Then some graph is constructed. Then it is stated that if
. Then some graph is constructed. Then it is stated that if 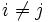 then ψi and ψj are in different right cosets. There is no reason that this should be so. In fact, since one can choose ψi and ψj arbitrarily subject to the condition that they are in different left cosets, it is easy to put them in the same right coset. -- Jitse Niesen (talk) 19:28, 6 August 2005 (UTC)
then ψi and ψj are in different right cosets. There is no reason that this should be so. In fact, since one can choose ψi and ψj arbitrarily subject to the condition that they are in different left cosets, it is easy to put them in the same right coset. -- Jitse Niesen (talk) 19:28, 6 August 2005 (UTC)
No, the proof of lemma 8 is correct, look at the original source [4].
The lemma 8 is a particular case of Hall's Marriage Theorem. The proof
in the particular case is exactly the same as the proof in the general
case. Rstewart 09:35, 7 August 2005 (UTC)
You can check Dharwadker's proof lemma by lemma, it is perfect! Rstewart 09:49, 7 August 2005 (UTC)
- I did look at the original source, I did check the proof lemma by
lemma, and I found a mistake in the first nontrivial proof of
Dharwadker's. I quote from page 17:
- "
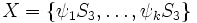 is the family of left cosets of S3 in Sym(ZN]S3) and
is the family of left cosets of S3 in Sym(ZN]S3) and 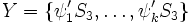 is the family of right cosets of S3 in Sym(ZN]S3). […] For any subset
is the family of right cosets of S3 in Sym(ZN]S3). […] For any subset 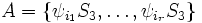 of X, one has
of X, one has 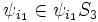 , …,
, …, 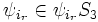 and there exist distinct
and there exist distinct  such that
such that 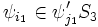 , …,
, …, 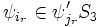 . "
. "
- My question is: why do these distinct
 exist? -- Jitse Niesen (talk) 10:44, 7 August 2005 (UTC)
exist? -- Jitse Niesen (talk) 10:44, 7 August 2005 (UTC)
See the wiki article on Hall's marriage theorem. A more general statement is true:
Let G be a group, and H be a finite subgroup of G. Then the marriage
theorem can be used to show that there is a set X such that X is an SDR
for both the set of left cosets and right cosets of H in G.
Although the wiki article does not provide a proof (perhaps you can add one), you can find a proof in:
ROTMAN, J.J. An Introduction to the Theory of Groups, Springer-Verlag, 1995.
Dharwadker's Lemma 8 is a special case with G=Sym(Z_N]S_3) and
H=S_3. I do not have a copy of Rotman's book with me at this time, but
I do remember studying the proof which is essentially the same in the
general case of any group G and a finite subgroup H. Rstewart 14:12, 7 August 2005 (UTC)
- I agree that the lemma is true, what I said is that Dharwadker's
proof is incorrect, which makes me even more suspicious of the paper.
-- Jitse Niesen (talk) 14:21, 7 August 2005 (UTC)
I think the proof of lemma 8 is correct (if you can check with the
standard proof of the more general statement). Are you sure that you
can say that distinct  do not exist? Perhaps your suspicions are unfounded? Rstewart 14:37, 7 August 2005 (UTC)
do not exist? Perhaps your suspicions are unfounded? Rstewart 14:37, 7 August 2005 (UTC)
- Yes, I am sure. However, I assume that Dharwadker can repair this,
as the statement of the lemma is correct (though it is puzzling that
neither the general case nor a reference is mentioned in the paper).
Jitse, I am beginning to seriously doubt whether you are sure of anything! It is obvious that the distinct  exist. It is a trivial exercise to show that distinct left coset
representatives always belong to distinct right cosets. Are you
familiar with elementary Group Theory?
exist. It is a trivial exercise to show that distinct left coset
representatives always belong to distinct right cosets. Are you
familiar with elementary Group Theory?
-
-
- For a counterexample to "Stewart"'s trivial exercise, see [5]. Cullinane 23:42, 8 August 2005 (UTC)
-
- No, you can always select left coset representatives such that
distinct left coset representatives belong to distinct right cosets. By
the way, are you the well-known crank Steven Cullinane? What have you
done now, proved that Hall's Marriage Theorem is false? Rstewart 11:38, 9 August 2005 (UTC)
You are giving me reason to believe that you are just picking a
lemma at random, picking a statement in the proof of the lemma at
random and claiming that it is false! The proof of Dharwadker's lemma 8
is correct. Every statement in the proof of Dharwadker's lemma 8 is
correct. And of course, Dharwadker's lemma 8 is correct. Rstewart 09:51, 8 August 2005 (UTC)
- So let us continue with checking Dharwadker's proof lemma by lemma, as Rsteward suggests.
Are you familiar with elementary group theory? You have just shown
above that you are not familiar with the elementary properties of
cosets!
-
-
- Again, see a counterexample to "Stewart"'s assertion at [6]. Cullinane 23:42, 8 August 2005 (UTC)]]
-
- Again, no, you can always select left coset representatives such
that distinct left coset representatives belong to distinct right
cosets. And again, are you the well-known crank Steven Cullinane? And
again again, what have you done now, proved that Hall's Marriage Theorem is false? Rstewart 11:38, 9 August 2005 (UTC)
-
-
- Click on "Cullinane" for my user page. You might consider setting up such a page for "Rstewart." For instructions, see User Pages.
-
-
- I respect Hall's theorem in all its variations. (By the way, there
is an excellent introduction to these variations in Balakrishnan's outline of combinatorics.) Cullinane 21:47, 9 August 2005 (UTC)
How are you going to check Dharwadker's proof? Rstewart 09:51, 8 August 2005 (UTC)
- Comparing Lemmas 9 and 12, we see something strange. Lemma 9 defines a function p and Lemma 12 defines a function π, but the definitions of p and π are the same (except that the roles of β and γ are exchanged).
So how are the definitions the same? You are saying nonsensical things! The domains of the the two are different! Rstewart 09:51, 8 August 2005 (UTC)
- Yet, π has order 2 where the order of p is unknown.
π has order 2 because the winding number around the branch point of
the riemann surface is 2. Are you also familiar with topology? Why do
you think the order of p is unknown? Ah, I forgot, because you are eminently well qualified in group theory! Rstewart 09:51, 8 August 2005 (UTC)
- In fact, π is ill-defined. We have (xpn)π = xp1 − n (last line of page 25), so xπ = xp (take n = 0) and (xp)π = x (take n = 1). The latter statement implies xπ = xp − 1. So what is xπ, is it xp or xp − 1? -- Jitse Niesen (talk) 17:01, 7 August 2005 (UTC)
Why ill-defined? Couldn't two things be equal in mathematics? Oh, yes I forget, you are also an expert in axiomatic set theory! Rstewart 09:51, 8 August 2005 (UTC)
Jitse, with the kind of arbitrary statements you are making, I don't
trust your judgement any more. Dharwadker's proof is correct. Rstewart 09:51, 8 August 2005 (UTC)
- I will leave it to others to decide whether I know enough group
theory, topology and set theory to check the proof. Here is my reaction
to your other comments:
- 1. In response to "It is a trivial exercise to show that distinct
left coset representatives always belong to distinct right cosets.": Is
it? Two of the left cosets of the group generated by the 2-cycle (1 2)
in S3 are { (2 3), (1 3
2) } and { (1 3), (1 2 3) }, so (1 3) and (1 3 2) are representatives
of distinct left cosets, yet they are in the same right coset.
To be fair to you, I should emphasize that it is always possible to
select left coset representatives so that distinct left coset
representatives always belong to distinct right cosets. In your example
, you can select (1 2 3) and (1 3 2) as left coset representatives and
they do belong to distinct right cosets. Rstewart 11:38, 9 August 2005 (UTC)
-
-
- I agree that it is always possible to select left coset
representatives so that distinct left coset representatives always
belong to distinct right cosets; my point is that that is not what you
said, nor what Dharwadker said in the paper. Jitse Niesen (talk) 18:37, 9 August 2005 (UTC)
- 2. In response to "The domains of the the two are different!": The domain of p as defined in Lemma 9 is T(β,γ) and the domain of π as defined in Lemma 12 is T(β,γ). They look pretty similar to me. So, where do I make a mistake?
Lemma 9 defines the domain of p as T(β,γ). Lemma 11 defines the domain of π as the complex plane C. The domain of p is a finite set. The domain of π is an infinite set. Rstewart 11:38, 9 August 2005 (UTC)
-
-
- I am talking about Lemma 12, where π acts on the set T(β,γ). I am claiming that action of π is the same as p. In fact, I don't see the point of Lemma 11; is it used somewhere in the proof of Lemma 12 or subsequent lemmas? -- Jitse Niesen (talk) 18:37, 9 August 2005 (UTC)
- 3. In response to "π has order 2 because the winding number around
the branch point of the riemann surface is 2.": This is the crux of the
problem. The construction of p and π has nothing to do with
Riemann surfaces or the graph embedded on the Riemann surface. Please
look carefully at the definition of p in the lemma and tell me: where is the dependence of p on the graph?
I don't see any graph embedded on the Riemann surface? What graph
are you talking about? If you are talking about the copies of the map
embedded in the riemann surface, then, sure, the domain of p is defined in their terms and π acts on the riemann surface. Rstewart 11:38, 9 August 2005 (UTC)
-
-
- Yes, I am talking about the copies of the map on the Riemann surface. How is the domain of p defined in their terms? You say above that "Lemma 9 defines the domain of p as T(β,γ)". Does T(β,γ) depend on the map? How? -- Jitse Niesen (talk) 18:37, 9 August 2005 (UTC)
- 4. In response to "Why do you think the order of p is unknown?": Because it is nowhere mentioned in Dharwadker's paper what the order of p is. Do you know what order p has?
Why should it be mentioned? Does anything depend on that? Rstewart 11:38, 9 August 2005 (UTC)
- 5. In response to "Couldn't two things be equal in mathematics?": Of course. So you agree that π is only well-defined if xp equals xp − 1 for all x, in other words, if p = p − 1? In that case, the paper needs to include a proof that p = p − 1.
Why? Does anything depend on that? Rstewart 11:38, 9 August 2005 (UTC)
-
-
- Everything depends on it. As I say above, if p ≠ p − 1, then the action of π is not well-defined, Lemma 12 is false, and Dharwadker's proof of the four colour theorem is false. -- Jitse Niesen (talk) 18:37, 9 August 2005 (UTC)
- -- Jitse Niesen (talk) 23:15, 8 August 2005 (UTC)
Another reason I don't trust your statements, Jitse, is that you
have claimed (not once but twice) that you had a specific
counter-example to the four color theorem. How can anybody believe
anything you say anymore? Rstewart 13:58, 9 August 2005 (UTC)
- Bob, it is no use trying to trick our readers into believing that
Jitse's claim was made as a genuine belief that he holds. Clearly,
Jitse was proposing the existence of a specific counter-example to the
four colour theorem to try to force you to explain why Dharwadker can
prove him wrong. This is a common method of argument in mathematics,
which seems foreign to you. May I remind you that I had to ask you
three times whether or not the map in question was a counter-example
before you admitted that it was not. Unfortunately, Jitse has failed to
force you into explaining anything at all, as have we all. Dmharvey
 Talk 20:57, 9 August 2005 (UTC)
Talk 20:57, 9 August 2005 (UTC)
Systems of coset representatives
In view of the discussion above between Jitse Niesen and "Bob
Stewart" about the conditions under which systems of common
representatives of left and right cosets exist, the following new claim
of Ashay Dharwadker is of interest:
"Using the axiom of choice, we prove that given any group G and
subgroup H, there always exists a common system of coset
representatives of the left and right cosets of H in G."
This is from Dharwadker's new web page Common Systems of Coset Representatives. Dharwadker's "proof" there is contradicted by a paper of Peter Schauenburg. For details, see my web page Coset Representatives: Two Opposing Views. Cullinane 20:23, 7 September 2005 (UTC)
Four-coloring of Jitse's second map
http://en.wikipedia.org/wiki/Image:Four-color-map.png
- Hi there Cahit. May I ask what the current state of that paper is? Has it been submitted to a journal for publication? Dmharvey
 Talk 23:57, 7 August 2005 (UTC)
Talk 23:57, 7 August 2005 (UTC)
- (by the way that was pretty cool. I was trying to figure out myself how to go about colouring the thing :-) Dmharvey
 Talk 10:26, 8 August 2005 (UTC)
Talk 10:26, 8 August 2005 (UTC)
Who's Cahit? Rstewart 14:50, 8 August 2005 (UTC)
Sorry, I see now, Cahit seems to have answered Harvey's question and found a four coloring for Jitse's second map! Rstewart 15:13, 8 August 2005 (UTC)
If Cahit's four coloring of Jitse's second map is correct, this
shows that Jitse's claim for his 5-colored second map was false (see
the section on "A further analysis of Dharwadker's proof" above).
Dharwadker's proof is correct. How many times did I say that Harvey? Rstewart 16:07, 8 August 2005 (UTC)
- Eleven times. Now, please answer my question, as stated above. Dmharvey
 Talk 18:59, 8 August 2005 (UTC)
Talk 18:59, 8 August 2005 (UTC)
A few more questions for bob/Dharwadker
- I have a few more questions about the structure and exposition of Dharwadker's "proof".
- (1) What is the purpose of introducing all the terminology and machinery of split extensions? In every case in Dharwadker's paper, the split extension being considered is really just a direct product.
(Dharwadker says so himself.) Why not just use the simpler language of
direct sums/products, which is no less expressive for the purposes
Dharwadker has in mind, and is certainly more accessible to the reader?
Is this a deliberate attempt at "proof obfuscation"?
- (2) Why is there no literature reference given for the result about
the existence of simultaneous coset representatives (Lemma 8)? I notice
that Rotman's book is listed in the references at the end of the paper,
but this reference is not pointed out near the statement or proof of
Lemma 8 itself. Is the reader supposed to read through all the
references to work out whether the result is Dharwadker's or is already
well-known? Either Dhawadker is assuming that the reader is already
familiar with the result and knows where to look it up (in which case,
why is he bothering writing out an (incidentally incorrect) proof?), or
it looks as if he is trying to pass off the result as his own, which
is, at the very least, highly unprofessional.
- (3) My earlier question, which I will not repeat here again, still stands unanswered. Dmharvey
 Talk 11:46, 10 August 2005 (UTC)
Talk 11:46, 10 August 2005 (UTC)
This page was last modified 23:08, 15 September 2005.
Cached page created Oct. 2, 2005.
Counter started Oct. 18, 2005.

![]() Talk 19:23, 3 August 2005 (UTC)
Talk 19:23, 3 August 2005 (UTC)![]() Talk 14:48, 4 August 2005 (UTC)
Talk 14:48, 4 August 2005 (UTC)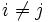 . Then some graph is constructed. Then it is stated that if
. Then some graph is constructed. Then it is stated that if 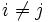 then ψi and ψj are in different right cosets. There is no reason that this should be so. In fact, since one can choose ψi and ψj arbitrarily subject to the condition that they are in different left cosets, it is easy to put them in the same right coset. -- Jitse Niesen (talk) 19:28, 6 August 2005 (UTC)
then ψi and ψj are in different right cosets. There is no reason that this should be so. In fact, since one can choose ψi and ψj arbitrarily subject to the condition that they are in different left cosets, it is easy to put them in the same right coset. -- Jitse Niesen (talk) 19:28, 6 August 2005 (UTC)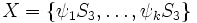 is the family of left cosets of S3 in Sym(ZN]S3) and
is the family of left cosets of S3 in Sym(ZN]S3) and 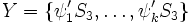 is the family of right cosets of S3 in Sym(ZN]S3). […] For any subset
is the family of right cosets of S3 in Sym(ZN]S3). […] For any subset  of X, one has
of X, one has  , …,
, …, 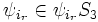 and there exist distinct
and there exist distinct  such that
such that 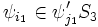 , …,
, …, 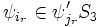 . "
. " exist? -- Jitse Niesen (talk) 10:44, 7 August 2005 (UTC)
exist? -- Jitse Niesen (talk) 10:44, 7 August 2005 (UTC) do not exist? Perhaps your suspicions are unfounded? Rstewart 14:37, 7 August 2005 (UTC)
do not exist? Perhaps your suspicions are unfounded? Rstewart 14:37, 7 August 2005 (UTC) exist. It is a trivial exercise to show that distinct left coset
representatives always belong to distinct right cosets. Are you
familiar with elementary Group Theory?
exist. It is a trivial exercise to show that distinct left coset
representatives always belong to distinct right cosets. Are you
familiar with elementary Group Theory?