Visualizing GL(2,p)

Steven H. Cullinane

Visualizing GL(2,p). Expository Note. March 26, 1985

"The typical example of a finite group is GL(n,q), the general linear group of n dimensions over the field with q elements." -- J. L. Alperin

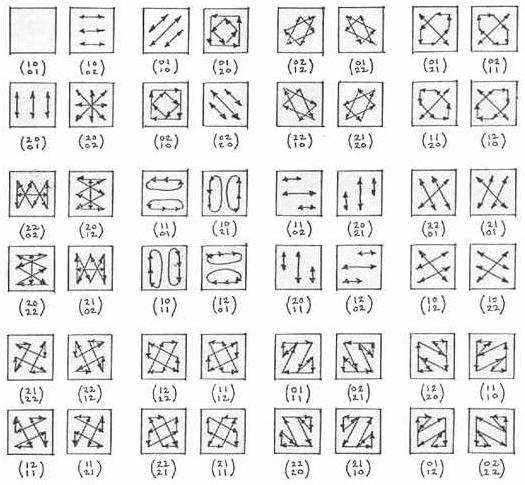
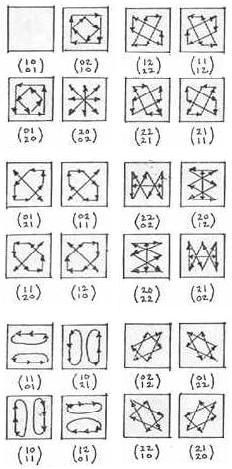
The 48 actions of GL(2,3) on a 3x3 coordinate-array A are illustrated above. The matrices shown right-multiply the elements of A, where

A = (1,1) (1,0) (1,2)
(0,1) (0,0) (0,2)
(2,1) (2,0) (2,2)

Actions of GL(2,p) on a pxp coordinate-array have the same sorts of symmetries, where p is any odd prime.

It is well known that the quaternion group is a subgroup of GL(2,3), the general linear group on the 2-space over GF(3), the 3-element Galois field.

The figures below illustrate this fact. (Here the "2" of the note above is replaced by its equivalent, modulo 3: "-1.")

The image “http://www.log24.com/theory/images/Quaternions2.jpg” cannot be displayed, because it contains errors.

The 24-Cell

Visualizing the
binary tetrahedral group
(the 24-cell):

The image “http://www.log24.com/theory/images/VisuBinaryTetGrp.jpg” cannot be displayed, because it contains errors.

The image “http://www.log24.com/theory/images/VisuBinaryTetGrp.jpg” cannot be displayed, because it contains errors.

Another representation of
the 24-cell:

The image “http://www.log24.com/theory/images/24-cell.jpg” cannot be displayed, because it contains errors.

From John Baez,
"This Week's Finds in
Mathematical Physics (Week 198),"
September 6, 2003:

Noam Elkies writes to John Baez:

Hello again,
You write:
[...]

"I'd like to wrap up with a few small comments about last Week. There I said a bit about a 24-element group called the 'binary tetrahedral group', a 24-element group called SL(2,Z/3), and the vertices of a regular polytope in 4 dimensions called the '24-cell'. The most important fact is that these are all the same thing! And I've learned a bit more about this thing from here:"

[...]

Here's yet another way to see this: the 24-cell is the subgroup of the unit quaternions (a.k.a. SU(2)) consisting of the elements of norm 1 in the Hurwitz quaternions - the ring of quaternions obtained from the Z-span of {1,i,j,k} by plugging up the holes at (1+i+j+k)/2 and its <1,i,j,k> translates. Call this ring A. Then this group maps injectively to A/3A, because for any g,g' in the group |g-g'| is at most 2 so g-g' is not in 3A unless g=g'. But for any odd prime p the (Z/pZ)-algebra A/pA is isomorphic with the algebra of 2*2 matrices with entries in Z/pZ, with the quaternion norm identified with the determinant. So our 24-element group injects into SL₂(Z/3Z) - which is barely large enough to accommodate it. So the injection must be an isomorphism.
Continuing a bit longer in this vein: this 24-element group then injects into SL₂(Z/pZ) for any odd prime p, but this injection is not an isomorphism once p>3. For instance, when p=5 the image has index 5 - which, however, does give us a map from SL₂(Z/5Z) to the symmetric group of order 5, using the action of SL₂(Z/5Z) by conjugation on the 5 conjugates of the 24-element group. This turns out to be one way to see the isomorphism of PSL₂(Z/5Z) with the alternating group A₅.
Likewise the octahedral and icosahedral groups S₄ and A₅ can be found in PSL₂(Z/7Z) and PSL₂(Z/11Z), which gives the permutation representations of those two groups on 7 and 11 letters respectively; and A₅ is also an index-6 subgroup of PSL₂(F₉), which yields the identification of that group with A₆.
NDE

Translation Plane

Figure A

From the website of

Priv.-Doz. Dr. H. Klein,
Arbeitsgruppe Geometrie,
Mathematisches Seminar der
Christian-Albrechts-Universität zu Kiel --

The Translation Plane of Order Nine

There are exactly four projective planes of order nine, and one of these planes is a non-Desarguesian translation plane.

Theorem. Up to isomorphism, there exists exactly one non-Desarguesian translation plane of order 9.

This translation plane is defined by a spreadset in a 2-dimensional vector space over the field GF(3), consisting of the following matrices.

As it turns out, the coordinatizing quasifield is a nearfield. Moreover the non-Desarguesian translation plane of order 9 has Lenz-Barlotti type IVa.3.

Two versions of the defining spreadset for this plane are shown in Figure A. In the left part of Fig. A, the matrices of Dr. Klein are altered by the use of "2" instead of "-1" (since these are the same, modulo 3). In the right part of Fig. A, the corresponding figures from my 1985 note Visualizing GL(2, p) are shown.

Page created August 28, 2005.